Solving an exponential equation with different bases
Vložit
- čas přidán 13. 05. 2022
- Here we will solve an exponential equation with different bases. We will solve 2^x=5^(x+2) by using the rules of exponents, logarithm, and the change of base formula. This algebra tutorial is suitable for Algebra 2 students or precalculus students. Subscribe to @bprpmathbasics for more algebra and precalculus tutorials.
Get a 1.618 t-shirt 👉 bit.ly/1618shirt
Use "WELCOME10" for 10% off
Shop my math t-shirts & hoodies on Amazon: 👉 amzn.to/3qBeuw6
-----------------------------
I help students master the basics of math. You can show your support and help me create even better content by becoming a patron on Patreon 👉 / blackpenredpen . Every bit of support means the world to me and motivates me to keep bringing you the best math lessons out there! Thank you!
-----------------------------
#math #algebra #mathbasics


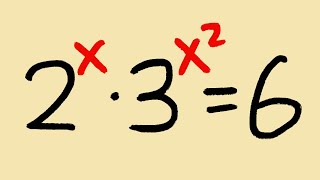






Interesting, I never knew you could do it that way. Here are my steps:
1. Take the natural log on both sides, & got: (x) (In2) = (x+2) (In 5)
2. Distribute: xIn2 = xIn5 + 2In5
3. Subtract xIn5 on both sides: xIn2 - xIn5 = 2In5
4. Factor the x out: x (In2 - In5) = 2In5
5. Divide: x = 2In5 / In2 - In5.
This works everytime for exponential equations with difference bases.
I did the same thing, that's how I usually deal with exp equations with different bases
I did it in exactly the same way!
Yes that’s how I do too
Something doesn't make sense... how is 2ln5/ln2-ln5 equal to 2log5/log2-log5 ???
@@silver3.593 They are equal. Both is equal to -3.513
u can actually also just do log both side right away and have:
x log 2= (x+2) log5
x log 2 = x log5 + 2log5
x log 2-x log5= 2log5
x(log2-log5)=2log5
x=2log5/(log2-log5)
First thought: 2 ^ any power is even and 5^any power is odd. Hmmm
Answer doesn’t have to be an integer
@@joaquinleon4114 yeh know that now 😥
Answer is -3.something I think
I got log base (5/e) of (2/25)
2power 0 is odd.
@@youben3468 but 0 clearly isnt a solution to this question
I enjoy learning math from you early in the morning and late at night, you're cool
朝闻道夕死可矣
That's kind of hot
@@lionelnelson2856WTF IS THAT SUPPOSED TO MEAN GOOGLE TRANSLATE???
An important point for students is to note that the reason we can divide by 2^x or 5^x, is that none of these can be equal to zero. Generally, however, when we divide by something that contains an unknown variable, we have to make sure to state it is different than zero and before we give our final answer, we check the case that it is zero.
any number different than 0 raised to any power is not equal to zero
I thank you for proposing these math problems, the solution to the second problem was -2log(6)/(log3-log2)
this has genuinely explained log rules better than my teachers in a few minutes so thank you so much
You are probably a genius who can understand a subject in a few minutes. The problem is and his teachers who don't know how to deal with your unusual intelligence.
But the important thing is that now, in addition to understanding the log rules, you also won some cookies on youtube. Good job.
I recommend this maths problem . This guy is crazy applied a method that I have seen before in CZcams .
czcams.com/video/z2OyVIJznHw/video.html
What’s interesting about this is that when you get to (2/5)^x=25. Intuitively, whatever number you choose for x will affect the fraction of 2/5. But the larger the number x is, the faster the 5 will grow in comparison to the 2. And you will never be able to find a positive value for x where 2^x/5^x=25 because the denominator will always be bigger. Then if we use exponent rules, we can realize that our x value will have to be negative. A negative x will swap the numerator and denominator and allow for the fraction to be equivalent, for some negative x value, to 25
Great intuition !
That's the correct answer.
Lol that's exactly right
For the last question, answer in the same format:
Step 1: 3^2x = 6^(x - 2)
Step 2: 9^x = (6^x) / 36
Step 3: 36 = (6^x) / (9^x)
Step 4: 36 = (2/3)^x
Step 5: x = logbase2/3(36)
Step 6: x = log(36) / log(2/3)
Step 7: x = 2log(6) / (log(2) - log(3))
Step 8: x = (2log(2) + 2log(3)) / (log(2) - log(3))
2log6/log2-log3 is it right ...
@@mathematicsbyraunaksir9778 👏👏
@@mathematicsbyraunaksir9778
No, it isn't. What you have written fails the BODMAS or PEMDAS test.
The answer from the post is incorrect.
As the OP solved the bases using the exponents first and that is really not the way to do it, you must put every one of the exponents at the start of the operation where they are conceived, for example:
3^(2x) = 6^(x-2) is equal to (2x)Log(3) = (x-2)Log(6).
From there you utilize distributive property, you group similar values and that's it, so, the correct answer is:
2ln(6)
x = - -------------------
2ln(3)−ln(6)
@@Lyonog- No, OP is correct.
Thank you so much! I was just looking for it!
x log 2 = (x + 2) log 5.
x log 2 = x log 5 + 2 log 5
x (log 2 - log 5) = 2 log 5.
x = 2 log 5 /(log 2 - log 5)
= 2 log 5 / log (2/5).
Evaluated:
x = -3.51294159.
good job!
You could type in log25÷(log2/5) and you would get this too
I want to do it without calculator
I thought of 2^x as e^xln2 and 5^x+2 as e^(x+2)ln5 and arrived to the same answer! Thanks to your previous teaching of course
For the question at the end I got 2(log6)/(log2-log3), which can interestingly be rewritten as 2*((log2+log3)/(log2-log3))
Okay.
Yeah, in more compact form you can write it as log_(6/9)(36).
@@williamhogrider4136 Okay.
2[log_3(2)+1]/[log_3(2)-1]
@@mynanstoenail6979 ok
We can simply make
Ln to the both sides so the exponents will get down
x.ln2=(x+2).ln5
This is so amazingly that everyone shouldn't complain about solving exponential logarithm with diff bases,but to be thankful...Thank you sir for this assistance once again.
The answer I got for the last question is -2ln(6)/ln(9)-ln(6), the exact answer is -8.838045165. In my opinion taking the natural log
of both sides for questions like this is very quick and easy to manipulate the equation to find x.
Agree
Problem with this you have the x+2 so if you started off with taking ln of both sides you'd end up with
xln(2)=(x+2)(ln(5)
Then it get's alittle hairy if you choose to continue down this path.
x/(x+2)=ln(5)/ln(2)
Multiply by (x+2)
x=ln(5)/ln(2)(x+2)
Distribute the fraction (ln5)/ln2)
x=xln(5)/ln(2)+2(ln5/ln2)
subtract( ln5/ln2)x from both sides to get
x-(ln5/ln2)x=2(ln5/ln2)
simplify the left to get
x[(ln2-ln5)]/ln2=2ln5/ln2
multiply by the reciprocal: (ln2/(ln2-ln5) and simplify
x=[2ln5/(ln(2)-ln5)], which is the solution, which in decimal form comes out to ROUGHLY -3.512941595.
Notice how hairy it gets? My first time doing it on the whiteboard function on my computer I forgot to subtract ln5 and put 5 so I got a screwy answer. Mind you it's 1:30 at night, but still. Sometimes doing work in the beginning to simplify before applying ln or log even (or having a fancy ass calculator and doing log base 2/5), makes things a whole lot easier. Way less steps and simplifying. It's hard for a lot of people to see ln(5)/ln(2) as a constant, but to do what you were heading towards you need to subtract that from 1 basically since you'll have x on one side and ln5/ln2 (x) on the other. Also, if you simplify ln(5)/ln(2), you'll make your final answer less accurate as more rounding produces more error.
I'd do exactly what he did except use ln since more calculators have ln and not a special log button where you can customize the base.
@@Tony29103 The way that I started the problem is by instead of dividing by x+2 at the start, I distributed the ln(5) to both values getting xln(2) = xln(5) + 2ln(5), I simply decided to subtract xln(5) from the right side and we get xln(2) - xln(5) = 2ln(5), I saw we could factor out the x so now we get, x(ln(2) - ln(5)) = 2ln(5), Now all we have to do is divide both sides by ln(2) + 2ln(5) to get a final answer of x = 2ln(5) / ln(2) - ln(5) which is the same answer you provided, just a bit less steps but I personally just find natural logs to be easier to work with. Thanks for your comment!
Well, I have done with another notation but i got the exactly same result, i guess its right so
@@Tony29103because thats not the best path. If you distribute the ln5 over x+2 and then move both x terms to one side, you can factor out the x and get the answer
Linguagem matemática é universal mesmo, entendi tudo sem entender uma palvra, ótima explanação. Grata.
Isso não é desculpa pra não aprender inglês não. Teria aproveitado melhor
@@igorcalvo Teria não, já disse que entendeu sem saber inglês.
Por isso a matemática é tão linda
Verdade.
Keeping my knowledge fresh as always.
I have been your subscriber for over 3 years now.
You inspired me to start my own channel
Ok but why do he have a pokeball doe
We don't ask that question here
Mikerfone
To keep the kids with a 5 second attention span engaged
He gotta catch em all
Thank you brother
Thank you. This was excellent.
I represented 6 as 3^log3(6), and compared the powers. X ≈ -8.83
Yea just write "APPROX" at end n everything will be O.K
Says my maths teacher
I got same answer but whenever I replace the X in Equation I don't get the same number on each side of the equation.
Interesting way of doing it.
Thank you for the nice lesson
Tks sit for this nice equation.Now here what would prompt you to apply logs while we normally use normal calculations
Your passion and enthusiasm are contagious. I always loved mathematics and would have loved to study it in its purest form. However I ended up in its applications. Nevertheless, I thoroughly enjoy your videos. :-) Keep up the good work.
I recommend this maths problem . This guy is crazy applied a method that I have seen before in CZcams .
czcams.com/video/z2OyVIJznHw/video.html
Heyyy
He is actually a good teacher
Equation: 3^(2*x)=6^(x-2)
1. ln both sides: 2*x*ln3=(x-2)*ln(2*3)
2. Develop and use ln properties: x*2*ln3=x*(ln2+ln3)-2*(ln2+ln3)
3. Isolate x on the left hand side: x*(2*ln3-ln2-ln3)=-2*(ln2+ln3)
4. Solve for x: x=2*(ln2+ln3)/(ln2-ln3) which can be written as x=2*ln(2*3)/ln(2/3), We see that x0 and the denominator is
It would be easier if you make it (9/6)^x
Sure @@user-nr2bf2jt5p , there are a lot of way to do so.
I apply log or ln on both sides first and then solve, but tysm for showing me a different method :)
The coolest part Is always the cute Little Pokéball in his hand. It's such a nice touch!
I love your videos. Thank you.
X=-8.838045... I think that is the solution
By simple algebra are they equal lhs and rhs. If not do you think you can make them equal by using log jugglers?
Just log both sides immediately with either a natural or common log and save yourself the trouble of a weird base. Distribute x+2 so you get xlog(5)+2log(5)=xlog(2)
Just get the xlog’s to one side, factor out the x
X(log(2)-log(5))=2log(5)
Then divide by everything other than X and that’s your answer without some weird base
Tell me if I am wrong with my solution:
2^x = 5^(x+2)
log 2^x = log 5^(x+2)
x.log2 = (x + 2).log5
x(log 2 - log 5) = 2.log5
x.log(2/5) = 25
And doing further calculation we can calculate x. Pls tell me if I am wrong here as it could help me develop my mathematical skills.🙂🙂
Good video for high school math!🤩🤩
To solve the problem you shared at the end 3^2x = 6^(x-2)
Log both sides and transfer the power to the left 2xlog3 = (x-2)log6
Expand 2xlog3 = xlog6 - 2log6
Group like terms on the same side 2xlog3 - xlog6 = - 2log6
Extract the factor from the left side x(2log3 - log6) = - 2log6
Find x x = -2log6 / {2log3 - log6)
I didnt get -2log6, instead I got it as positive.
Thanks. That was fun. It has been a long time since I used log functions. Forgot how, LOL!
Excellent sir..
I did it a different way and didn't need a calculator to solve it.
I converted both sides to log10 and substituted the bases.
2=10^.3 and 5=10^.7
That left a simple algebra problem .3x=.7x+1.4. This simplifies down to x=-3.5.
-2log6/log3 -log2 is the answer for the last question
so helpful
3²ˣ = 6ˣ⁻²
Expand the right side.
3²ˣ = 6ˣ(6⁻²)
Divide both sides by 6ˣ.
3²ˣ/6ˣ = 6⁻²
Simplify.
(3²/6)ˣ = 1/36
(9/6)ˣ = 1/36
1.5ˣ = 1/36
Take the log base 1.5 of both sides.
log₁.₅(1.5ˣ) = log₁.₅(1/36)
x = log₁.₅(1/36)
Use the change of base formula.
x = (log 1.5)/(log 1/36)
Expand the denominator (and numerator if you kept 1.5 as a fraction).
x = (log 1.5)/(log 1 - log 36)
Simplify.
x = - log 1.5 / log 36
2xln3=(x-2)ln6>>>xln(3/2)=2ln(1/6)>>>>X=ln(1/36)/ln(1.5)=log to the base 1.5.(1/36) ...so simple no need to apply so many steps
@@RakeshKumar-rc4sj Still simplier is after taking log to base 10 both sides, convert it in to equation of 1 st degree and simplify it.
@@Uma-Bharat-India What does "equation of 1st degree" mean?
Despite learning this multiple times throughout my lifetime, I never retain any memory from my math classes
Very good question sir.
I'm a new subscriber. Just one question, do you have a video abt logarithms? If you don't have it, can you make a video abt it? I haven't seen that before.
Please explain the line number 3
Nice work.
I get log(3/2)(1/36) for the one at the end.
Or -2log(6)/log(3)-log(2)
What about taking Ln?
I found a formula which states ..log base 1/n of a = n log (a) ...is it correct ?
Gotta Solve ‘Em All
We can also take the ln on both sides.
Hello sir... I've not understood how you have cancelled the log 5 with denominator of log2-log5.. whereas we have negative sign before it... please elaborate
I still haven't learnt what log is yet or any of this in school but it looks fun so I'll learn it early
(2/5)^x = 2^2
Taking log to the base 2 one gets
x* ( 1 - lg(5) ) = 2
or x = 2/( 1 - lg(5) )
(2/5)^x would be 5² not 2²
Could of used log from the very beginning to bring the exponents down.
Is anyone calculate by changing any number n to (e^ln(n)) first?
I did by integrating both sides wrt dx
answer for the next question :
3^2x = 6^(x-2)
taking log on both sides :
log(3^2x) = log(6^(x-2))
2xlog(3) = (x-2)log(6)
2xlog(3) = xlog(6) - 2log(6)
2xlog(3) = xlog(3) + xlog(2) - 2log(6)
x(log(3) - log(2)) = -2(log(6))
x(log(3) - log(2)) = -2(log(3) + log(2))
x =-2(log(3) + log(2))/(log(3) - log(2))
here log can be replaced with natural log.
Hope its correct.
The main way I do it (I don't know if this is the most efficient way) is log both sides of the equation, move the exponent to the front. The equation for this scenario currently would be x(log(2))=x+2(log(5)). Divide either log on both sides of the equation. (For this equation I did log(5)/log(2)). After this you are left with x=x+2(log(5)/log(2)) or x=(roughly)2.32192x+4.64385. Subtract x from both side which leaves you with 0=1.32192x+4.64385. Subtract 4.64385 from both sides then divide by 1.32192. This gives the answer -3.512958, its not exact, (off by around 1/10,000 but it would be exact if you either use the ans key or write out the entire decimal.
I just multiplie the power of the base 5 by log2(5) then let the exponent of LHS = the exponent of RHS
In last we can put values of log on base 10 which is log5= 0.698, log2= 0.3010, log3=0.4771 🇮🇳
I did this instead...
3^2x = 6^(x-2)
Taking log of each side
2x log(3) = (x-2) log(6)
Subtract x log (6) from both sides
2x log(3) - x log(6) = -2 log(6)
Take advantage of 2 log(3) = log(9) and -2 log(6) = log(1/36) To clean things up a bit
x log(9) - x log(6) = log(1/36)
Combine log(9) - log(6) to give log(9/6), which is log(3/2)
x log(3/2) = log(1/36)
Divide both sides by log(3/2)
x = log(1/36) / log(3/2)
Apply quotient rule to all logs, and multiply numerator and demoninator by -1.
x = log(36) / (log(2) - log(3))
Before we start, is a PokeBall required to solve the equation?
What is it for
I always used natural log because Ln is shorter then log and doing that over a half page of more complex problems saves time
I recommend this maths problem . This guy is crazy applied a method that I have seen before in CZcams .
czcams.com/video/z2OyVIJznHw/video.html
Is there a way to solve 2^X = 57^X+1? How about Squrare root X= X^3 solve for X?
How about 2/(log5(2)-1)?
2log(6)/log(2) - log(3)
The answer to question given by you at end is x = log2/3(36)
This is my first time being introduced to log. Seems simple enough. I just have to practice. Thank you.
Hello,
I wanted to kindly remind you that I sent you a message regarding your videos.
Do we have your permission to use them?
We would be happy to know if there is any special requirement for publishing your videos that we could fulfill.
Thank you! :)
Sincerely,
Divya
hah ignored
Fr
Depends what you mean by publishing. Using it in the classroom is probably ok. Profiteering out of it is probably not.
Upload more exponential question
in the old days before slide-rules even, we had to use log tables, so I know that log(2) =0.3010 and so log(5)=0.6990
so taking logs
0.301x = (x+2)(0.6990)
0 = 0.398x + 1.3998
x=-1.3998/0.398
x= -3.5170
"Before slides rules" - There's no one that old anymore. Before calculators, sure!
@@jrkorman you are wrong. slide rules came in in the 1960s. I learnt to use them in 1965/6. before that we used 4 figure log tables instructed by Brigadier Frank Picton, who said when he was.working of the Army Ordnance Survey in the Punjab, he used 7 figure logarithms.
both log tables also had combined trig functions such as log.sin.
much needed when using the sine rule when triangulating the territory.
@@davidseed2939 Google is your friend (sometimes). In this case - "Slide Rule History" From one source
"The slide rule was invented by William Oughtred in the 1600’s, but only began to be widely used in the mid 1800’s after a French artillery officer named Amedee Mannheim developed a version that became popular among engineers. By the early 1900’s engineering students in the US were commonly taught to use slide rules. They continued in widespread use until the late
1970’s when electronic pocket calculators became available."
@@jrkorman i am telling you of my experience in England. If American school children used slide rules earlier than me, fine. Doing my final exams at university in 1972. One person had a calculator. They were very expensive and used reverse polish operation.
(eg 5, store, 6, multiply.. result 30)
@@davidseed2939 My first experience of using an electronic calculator was also during my first year at university (Auckland, NZ) in 1972. It was a Hewlett Packard and was screwed down to a bench in the Physics Laboratory. Students had to book time to use it ... and there was generally a queue. I still prefer RPN (reverse polish notation) and use it on my own HP calculator which I bought in 1990 and which still works perfectly.
The final answer is x= -3.5
Why dont you just replace the base with e^ln(base). Then equate the two exponents and solve for x?
2^x=5^(x+2)
Applying log(natural log) on both sides
x•log2=(x+2)•log5
x/x+2=log5/log2
x/x+2=log base2(5)
x=x•log base 2(5)+logbase2(25)
x•{logbase2(2)- logbase2(5)}=logbase2(25)
x=logbase2(25)/logbase2(2/5)
x=logbase2/5(25) solved
This question is solved using property
logbasea(b)=logbase c(b)/logbase c(a)
you are right this method is very easy
We can use only property for Naperian logarithm (Ln a^x = x Ln a )
natural log is ln
Log_6/9(36) for the end question
Nice
yeah same as log 2/3 36
x=-2log(3/2)(6)
An exponent divided by an exponent doesn’t cancel the exponent? 4/25=625?
In last question,
x = [2log6/(log6 - log9)]
I just taught this to my summer school algebra 2 class.
Easer if we take "ln" to both hand sides
For the last one x= -log(36)/(log(3)-log(2))
Nice video 💖💖
x=2(ln5/ln2)/(1-(ln5/ln2))
first equation
for the question at the end:
x=log3/6(6^(-2))
Why log exists for any number?
Just ln() both sides and solve for x. xln(2)=(x+2)ln5 x(ln(2)-ln(5))= 2ln(5). x=(2ln(5))/(ln(2]|ln(5)). Seems easier.
Xf que alguien me diga que temas uso para poder entender
Simply take log of both sides first and then solve. Much easier. X log 2 equals (x+2) log 5
heres my method and its a little wierd
3^2x=6^x-2
3^2x=3^log3(6)(x-2)
same bases so equate powers
2x=log3(6)(x-2)
2x=xlog3(6)-2log3(6)
2x-xlog3(6)=-2log3(6)
x(2-log3(6))=-2log3(6)
x=-2log3(6)/2-log3(6)
x=-8.838
2log6 /log 2 -log 3 is it right or wrong ..
Thank the heavens for numerical methods. There is no way I could have solved this. 😆
idk but i am feeling proud after solving it myself
For the assignment question, the answer is x= 2 log 6/(log 2 - log 3)
What is that red and white ball in his left hand?
What is the purpose of it?
x=log25 with base: 2/5