the most controversial limit in calculus 1
Vložit
- čas přidán 1. 11. 2020
- Why we cannot use L'Hospital's Rule for the limit of sin(x)/x as x goes to 0. This limit is first taught in calculus 1 while doing the derivative of sin(x) by using the definition of the derivative.
"The Limit" • The Limit (do not use ...
The shirt: teespring.com/cute-math-cat-17
Subscribe for more math for fun videos 👉 bit.ly/3o2fMNo
💪 Support this channel, / blackpenredpen
🛍 Shop math t-shirt & hoodies: bit.ly/bprpmerch. (10% off with the code "WELCOME10")
🛍 I use these markers: amzn.to/3skwj1E
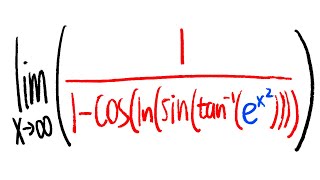






Come on its clearly approaching 1. Using the fundamental theorem of Engineering, sin theta is simply equal to theta. Therefore, theta / theta = 1.
I see what you did there
but its a fact thats comes from taking first terms from taylor series for sin, which requires differentiating sin, otherwise I dont think theres a reason for thinking sinx is approx x for small values
by the way, he say it in the video..
Te ves muy fresco 😎👌
yeah, and limit just means evaluate at the point
I will never not read l’hopital as “le hospital 🚑🏥🥼” 😂
@hawkturkey 🙈🙈🙈
You will never “not” read lollll
@@blackpenredpen hahaha never not, (two negatives together make one positive)
Btw, excellent video respected Sir,
Muhammad Hussain Sarhandi Several languages commonly use the double negative as an emphasis, rather than the apparent literal meaning
this
I just used this as an example of when to use L'Hopital's Rule when tutoring someone yesterday 😳
F
@@bugraaydn3602 Think about it this way: 64/16 = 4/1. Just cancel the 6 on the top with the 6 on the bottom and you gwt your answer. Is this correct? Well, no. You get thw right answer, the method is easy to describe, but that doesn't mean applying the method here is correct just because it gives a correct answer. Similarly it is with lim as x->0 of sin(x)/x, if you use L'Hopital's rule to get it is the wrong method because you can't understand how to get the derivative of sin(x) without understanding what the answer to limit as x->0 of sin(x)/x (try and derive it using the limit definition of a derivative and prove it yourself). This means when you use L'Hopital's rule here, you are assuming the answer to the limit before you make it in a subtle way, and if you assume the answer before starting you haven't really worked it out. For other limits you apply L'Hopital's rule to, you don't tend to run into similar issues and it essentially is just due to the properties of the sine function in particular.
@@bugraaydn3602 In order to find that its cos you need to know what he is trying to find out
M a physics guy but love this fella
*oh frick*
Lol when I saw cosh, I was confused for a solid 5 seconds trying to figure out where the hyperbolic functions came from.
Me too lmao
just use the fundamental theorem of engineering: sin(theta) = theta for small angles of theta
= theta/theta = 1
It depends on your definition of the sine function; this argument only works if you define the sine function through angles and the unit circle. However, in order to even rigorously define what an angle is, you have to use either the complex exponential, measure and integration theory, or another tool in this lane; from a mathematical standpoint, it is not at all clear what it means for a circular segment to have some length. For the sake of simplicity, most analysis textbooks define sine and cosine via the exponential function or via their Taylor series expansions; in both cases, the derivative of sine being cosine follows very easily from differentiating the power series in question term by term, which is alright because it has an infinite radius of convergence (and power series can always be differentiated term by term within their open disk of convergence).
Exactly. Couldn't have put it better myself 👍🏻
This guy probably has more students cheat off of him than girls cheat on him... and that's okay bc I'm both a virgin and an idiot
edit: or girl. or other.
Could you provide additional information about this topic? I'm interested
@@ginosuinoilporcoinvasivo8216 If I may ask, what exactly would you like to know more about? The complex exponential? Measure theory? Defining sine and cosine via their power series expansions?
@@ginosuinoilporcoinvasivo8216 It all depends on your definitions. There is lots of areas (particularly in pure mathematics such as analysis) where you need to be incredibly precise with your definitions. For example we all know that sin(theta) can be considered as "opposite/hypotenuse" or as a power series, and we'd hope that these two notions are equivalent (but starting only from the power series, it isn't obvious that it has anything to do with triangles and equally starting from the triangle it's not obvious it would even have a power series!).
This is often the case, there are different definitions of integration that each apply to a certain class of functions, and we hope that when we consider two different definitions of integration considered on the same function for which the definitions make sense, we hope that they would agree (which they infact do). This is the idea behind Lebesgue integration (involving measures) as a more general form of Riemann integration (the typical "area under the curve" approach).
That got very long winded and philosophical, but I hope it made sense! Loads more examples come up in Complex analysis when you can start from different definitions and propositions and still unlock the same theorems.
Hope this helps
Yeah my calculus teacher couldn't explain why so thank you
I feel like the table of values method might be more egregious, because it’s not an actual proof and you don’t know the true limit
and you're left with the question of how the table values for sin(theta) were created in the first place? Taylor expansion or its cousins?
I learned in the Analysis I class that the trigonometric functions are defined by:
sinx:= x/1! - x^3/3! + x^5/5! - ...
cosx:= 1 - x^2/2! + x^4/4! - ....
So d/dx(sinx)=cosx. So I can use LH rule...
These definitions assume that the derivatives of sinx and cosx are cosx and -sinx respectively.
@@aram9167 No. We are not calculating the Taylor expensions here. We're only taking these two series as definitions for sin and cos
Just as the exponential function is often defined by it's series as well.
It then follows that the derivative of sin is cos
It's only the power rule
--
Note that you can also define sin and cos with the exponential
It also follows that the derivative of sin is cos
These functions can be shown to come from the Taylor series, can they be derived another way? We can show lim n->inf (1-1/n)^2 gives the Taylor series for e....
The problem is that if you define them this way, you can use LH rule, but you don't know if they match up with circle angles and such. You need to prove a lot of the inherent properties exist as well, like periodicity and convergence (perhaps not too hard, but necessary).
Even if they share some of the properties, you still need to show that they are equivalent to the sin and cos functions defined by using circle angles, if you want to use them for that type of analysis.
It's a bit of a trade off. You have an easier time proving the limit sin(h)/h, but you need to show it's a well behaved function and that it matches up with circles afterwards.
@@zapzya See the top comment above. It's hard to rigorously define angles and lengths for curves. In particular, here's a fun question. What's pi? The ratio of the radius of the circumference of a circle and its diameter? What's a circle? You basically took a broom and swept a transcendental series definition underpinning sine and cosine into a number called pi and just decided to symbolically manipulate it. You don't get periodicity, convergence or anything else automatic. You just a priori assumed it would work just because you could draw a circle. Does that work on any underlying field other than reals? That's why most analysis classes start with a series definition of exp(x). It's not the Taylor series for e^x. It's the definition of the exp operator. It works for matrices. It even works for the exponentiation of operators (when you start fiddling with Lie groups and algebras). You later show that the Taylor series is unique and immediately conclude that this definition of exp must coincide with its Taylor series.
At my university sin(x), alongside exp(x) and cos(x), was defined as the (Taylor) series before the concept of Taylor series was introduced for more general functions.
6:55 I'm glad you noticed that after "don't" you can not have "neither" :D
Always improving :)
Thanks 😊
real physicist like me just uses the small angle approximation and writes θ/θ
guess i'm just different 🤷🏻♂️
That is exactly Using Taylor’sexpansion . I think this whole video is wrong.
@@idjles according to this: ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/unit-5-exploring-the-infinite/part-b-taylor-series/session-99-taylors-series-continued/MIT18_01SCF10_Ses99c.pdf
you have to know how to derivate sin(x) before going Taylor. I think your whole comment is wrong
not sure if you are joking, but this approximation only works because we know that the limit of sin t / t is 1
@@nasekiller demonstrate it without l'Hôpital's rule
@@tomasbeltran04050 how you show it, is completely irrelevant. But you can only use the Approximation sin t = t for small t, because the limit of sin t / t is 1
you can’t stop me!! MUA HUAHA
😂
😂 😂
😂 😂 😂
Judging by his replies, I'm pretty sure he is mad.
@@jhanzaibhumayun5782 pretty weird replies
so cool, didn't know that. And now to find the geometry demonstartion of the limit (thanks for adding it on the description)
As a high school student, I only know so little, but I really love using the squeeze theorem to prove it approaches 1. Even though it takes more time, it's much more satisfying for me.
Exactly that level of satisfaction after solving a complex limit 🤩
I just find it so funny that you begin releasing videos on topics that I begin to learn that very week! Thank you so much!!!
i love how this video turns up the day we go over l’hopital’s rule. and our first example was sin(x)/x 😂
In complex analysis I actually use L'Hospital's rule for lim (z-k)*cot(pi*z) as z approaches an integer k so that the cosine in the numerator cancels with the cosine (derivative of sine) in the denominator. This limit is often used in the calculation of difficult series. Another reason to use L'Hospital's rule is for something like lim (z - exp(pi/4*i)) / (z^4 + 1) as z approaches exp(pi/4*i). The reason is that it's far easier to enter a single value into 4*z^3; factoring the denominator and cancelling makes it nasty after taking the limit.
I think 3Blue1Brown did a geometric proof for the derivative of sin(x) with respect to x, without using the limit definition. With the geometric proof for the x-derivative of sin(x), I am not sure if using L’Hopital’s Rule in this case would still be circular reasoning.
czcams.com/video/S0_qX4VJhMQ/video.html
I think this is only circular reasoning if you use those particular proofs of dsinx/dx=cosx/taylor series of sinx as "the proof".
For example, I could derive the taylor series by using the series for e^(ix) and Euler's formula from complex analysis. This does not require previous knowledge of the limit.
But how has Euler's formula been proven?
@@Apollorion there are some awesome proofs that don't use the taylor series of sinx,cosx,e^x
@@hybmnzz2658 That's an ambitious claim which would be nice to be true.
Can you quote such a proof or provide us a link so that we can verify?
Here are a bunch math.stackexchange.com/questions/3510/how-to-prove-eulers-formula-ei-varphi-cos-varphi-i-sin-varphi
Some of the proofs rely on the derivative of sinx though so be careful.
Some more noteworthy mentions: -arguing that e^ix represents an object whose velocity is always normal to it (hard to explain it has a physicists intuition)
-mathologer has a video on e^ipi for dummies where he shows e^ipi=-1 using only the properties of complex multiplication and the limit definition of e. I think when generalizing and rigourizing this it becomes a problem though as you may need sinx/x limit anyway.
Imagine finding more complicated proof of d(sin x)/dx = cos x that doesn't rely on knowing the value of lim x -> 0 for (sin x)/x just to make sure using L'Hopital rule for lim x -> 0 for (sin x)/x won't cause the trouble of circular reasoning
It depends on how you define sin(x). The definition given in Rudin's Principles of Mathematical Analysis of sin is its power series expansion. Then you can define pi as the smallest positive value for which sin(x) = 0. And you can describe sin's geometry directly from the Fundamental theorem of Trigonometry sin^2 + cos^2 = 1
Is there any relationship between the summed angle sin formula with the product rule? They look so similar to one another!
The fact you can find a circular argument for a conclusion does not make the conclusion invalid, it makes only this particular argument invalid.
Yes, and that is exactly why it is incorrect to use L'Hopital's rule here. Maths questions are not about simply giving an answer, but demonstrating an understanding, show your work etc.
@@Jordan-zk2wd So where do you end? You would prefer to start with Hilbert's Principia to arrive at 1+1=2 on page 160 or so, and take it from there? You would hardly get anywhere in your entire lifetime. Here, the validity of l'Hopital can be shown by applying the definitions of a derivative (in terms of a limit), but the point is that that would work with any ratio of two continuous and differentiable functions that approach zero (whether sin(x)/x or x^2/tanh(x) or anything similar), and that IS De l'Hopital's rule.
Not allowing De l'Hopital here is akin not allowing functions of real numbers until you show that you understand those properly too.
It is perfectly fine to build on proved work of others. If we can see further it is because we stand on the shoulders of giants, and such.
@@landsgevaer the reason for not using l’hopitals here is that it involves computing the derivative, whose computation in turn relies on the limit being well define. This is why the logic is circular. It does not mean we have to go all the way back to the axioms to justify anything; we just can’t have something being true because it is true because it is true because it is true because it is true ad infinitum
@@numbers93 But wait, these are different limits!? If it had said sin(x)/x^2 then the derivatives of the numerator and denominator do exist, but the limit of the ratio doesn't; contrariwise, if it had said |x|/(|x|+1), then the derivatives don't exist but the limit of the ratio does. These are different things. Both are limits, but entirely different limits. So how can it be circular!?
@@landsgevaer what are you on about? what do the existence of the other two limits you are introducing here have to do with the circular logic illustrated by the video regarding the proof of the limit of sin(x)/x?
i'll just use the small angle approximation-
"No Taylor Series!"
proof by graph: you can see its close by seeing the graph
Q.E.D
The small angle approximation for sine comes from the Taylor series, which explains how we know it is a first order approximation. That for the cosine derives from the same source, which shows it is a second order approximation, which in turn explains why the cosine approximation for small angles is so good.
@@johnnath4137 that was the joke. He said “I’m gonna use small angle approximation but not a Taylor series” as a joke because some people would probably say that unironically, without realizing the small angle approx is literally an application of the Taylor series.
@@johnnath4137 how do you know that . What if Taylor series started from the understanding of the small angle concept in the first place ?
@@Beny123 I see where you are coming from. Historically, the trig functions emerged from geometry, and the small angle approximation was known well before the advent of calculus and the Taylor series. But the geometrical ‘proof’ of the result is not rigorous and is not good enough for a modern proof. The root of the trouble is that the simple geometrical definitions of the trig functions are themselves wanting in the requisite rigour. Possible ways of supplying this rigour is to define these functions in terms of integrals (as has been done by G H Hardy in his seminal A Course of Pure Mathematics) or in terms of power series (after the manner of Karl Weierstrass). Unfortunately, this means that a rigorous treatment of the trig functions has to be delayed until one is well into a first course of real analysis. In this approach, the limit of (sinx)/x as x → 0 is trivially 1: simply divide the power series for sinx (which you will note constitutes the definition of sinx if we use the Weistrassian approach) by x and substitute x = 0. Of course this all presupposes that the whole theory of the convergence of power series has been previously set up. The integral approach of Hardy is even worse: here the theory of Riemann integrability needs first to be developed. But it is right that school age children should be introduced to the trig functions via geometry and that they should be shown the intuitive plausibility of the small angle approximation. But when it comes to strict proof of results, the trig functions need first to be re-defined analytically.
2:22 This is why I write the parentheses. No need to worry about confusion because there is none.
I should have done that!
It reminds me of the time doing series
Sin(n)/ln(n)
And you can imagine how bad it would be with out ( )
@@blackpenredpen sinn/lnn well obviously the two n's cancel out so its si/l but as we known from Roman numbers L is fifty and i is the imaginary unit so sinn/lnn is i/50s
@@blackpenredpen Oh it’s not just you. All my math profs would omit parentheses. It’s not so bad here because “sinh(+)” doesn’t mean anything, but it drove me nuts in classes where we had stuff that should’ve been written “sin(h)*x”, and because people also like to omit the “*”, it’d get written sinhx and you had to just magically know if the prof meant sinh(x), sin(h*x), or sin(h)*x. Heaven help you if there was also a variable “hx”, because there was at _least_ a 50/50 chance that the prof would be in such a habit of omitting the “*” that they’d write “h*x” as “hx” even though they’d already said “hx = h+x” or whatever earlier in the problem.
and we usually write function arguments in parentheses, e.g f(x). Wonder why people decided they don't have to do it for trigonometric functions. Would it be acceptable to write fx = x² for example?
This is a very eye opening video... I always knew Lim x-->0, sinx/x was a tricky limit but now it's clear why
I never considered the circular logic in applying L'Hopitals in situations like this; thanks for sharing!
there is a powersum of sin(x) =x-x^3/6+x^5/120...
divide it by x will result in 1-x^2/6+x^4/120...
If we are working with circles we can find that the derivative of a circle e^ix = cos x + i sin x is just i*e^ix = i cos x - sin x, therefore the imaginary parts show us that (sin x)’ = cos x without limits.
Correct me if I’m wrong but doesn’t it depends of the definition of the sine function ? I mean , if it’s defined as its taylor series then we can use l’hopital, excuse me if it’s not clear
Instead of using the Hospital rule u can use the Taylor series to calculate the limit.
Sin (x )/x = (1/1! .x¹ - 1/3℅.x³ + 1/5! x^5 - ....) /x = 1/1! - 1/3!x²+ 1/5! x⁴ - .... And here all terms except the first term tend to zero as they have x. Abd the first one is 1.
It's not necessarily circular reasoning since you can prove d/dx(sin(x))=cos(x) with methods different than the limit definition of derivative.
What other method we can use?
Geometric
"methods different from the limit definition"
To be clear, the limit definition is the only definition. Every single method for evaluating derivatives relies on what a "derivative" is.
@@justacutepotato2945 you can define the sine function as a taylor series and then calculate the derivative using the power rule, or you can also prove that the rate of change of the sine function is equal to the cosine using geometry, or you can calculate the derivative numerically substituting values, or you can also define the sine as an inverse function of an integral, or well, you can also define sine as the function whose derivative is cosine. And those are only a few examples: no need to know the limit, no circular reasoning
@@lagrangiankid378 won't there be like only one conventional single for the definition of sine?
I read a paper about education. Conventional method to prove the limit of sin θ / θ, using area properties on a circle, is also a logic circulation, because the area's strict definition needs an integral of sqrt(1-x^2). The problem is, it requires calculus of trigonometric functions. So maybe the most rigorous way is to define sin and cos as their taylor series.
Can you make the geometric proof for this? That would be awesome to see and understand.
As soon as I saw theta as the denominator, I knew what was about to happen. My calculus teacher in college told me if I ever saw that, to do what you said to do at the end. He actually did a great job going through the problem too cause I was confused as hell at first.
Hey BPRP, would love some help with this calc 3 problem!
∭(𝑥−2)𝑑𝑉
V
where
𝑉={(𝑥,𝑦,𝑧):((𝑥−2)^2)/9+((𝑦+3)^2)/25+((𝑧+1)^2)/16
For the derivative of sin with the lim. U can use also the formula of simpson to do the top of the fraction.
The lim (x>0) of sin(x)/x is the same thing to the lim (x>0) of (sin(x) - sin(0))/(x - 0)
In other meaning it's the definition of the derivative of sin(x) when x=0
So we can just derive sin(x) which is cos(x) and calculate cos(0) which is 1 . And that's it.
But d/dx sin x = cos x is something you get FROM the limit, so you can't use it to prove the limit itself, that's circular reasoning.
It is only circular if we use l'hopital's rule or Taylor series to find d/dx sin x itself.
Once we have found that d/dx sin x = cos x by some other means we can freely use this in future l'hopital's rule or Taylor series calculations.
I used the sum to product formula and ended at cos(theta)*(lim h->0 sin(h/2)/(h/2)), similar technique can be used for the cosine function
How about using the squeeze theorem? That’s what I did for my previous problem set
What if you differentiate sin(x) in its complex form? Can LH be used then?
i dont know how it was for you, but when i had calc 1, we actually defined sin and cos via a power series. if you do that, you can easily see that sin' = cos by differentiating each summond individually.
Where can i get that derivaties list on the right of the white board?
My Teespring link is in the description. It’s called the “derivative on your wall”. I am also doing a 20 off discount with the code “superfan20” from now to thanksgiving. Thanks.
sir, can we apply L Hospital rule for lim x-0 (tan x)/x
Best explanation ever. I looked for this from my university years... :)
If we prove that the derivative function of sin theta is cos theta by differentiating the power series expansion of sin theta, can we use l'hopital's rule?
How about defining sintheta in terms of (e^(i theta) - e^(i theta))/2i ? That will also do it shortly.
e^(ix)=cos(x)+isin(x) is derived either from Taylor series or differential equations, so no.
@@aram9167 I thought they were just derived from hyperbolic trigs. I guess i was wrong
@@aram9167 Well yes. And no.
You can use the series as DEFINITIONS of sin and cos
The same goes for the exponential function.
Then you can prove that e(ix)=cos(x)+i.sin(x)
Without knowing any derivative
--
In fact, if you define sin and cos by their series, it immediately follows that the derivative of sin is cos 🤷
@@Kerlyos_ The issue here is that bprp defines sine as being the y-coordinate of the unit circle, no?
You can define it with power series, sure, but that definition just seems completely arbitrary and nonsensical compared to the geometric definition.
@@Kerlyos_ but to define the series expansion you must know the derivative in first place (and probe that cos(x) is actually the derivative) so... no, you can't define sin(x) and cos(x) with its series *if you want to probe the derivative of sin(x)*.
Either way, yeah, of course you could do that
You can dimostrate the limit with the definition of the taylor serie of sin(x). And working with that by multiplying with 1/x which is the denominator
For some reason, l’Hopital’s Rule isn’t taught in France. We only use the limit of the rate of change (not sure that’s the right name).
Wait why?! Isn’t Guillaume de l’Hôpital French?
Hmmm , I can tell it’s told ! But as far as I know, our teachers want us to use limited development (wich is actually the same)
@@Ben-wv7ht Actually I spoke without knowing. I’m only in first year of prépa, and I believe we’ll only learn about limited development at the end of the first semester (outside of physics/engineering).
Still, I skimmed through the limited development chapter and it seems like they never present it as L’Hopital Rule.
@@blackpenredpen Yes he is, and indeed L'hospital was publied by him but it was Johann Bernouilli (a Swiss mathematician) who probably invented this method.
In fact in France we prefer use a Taylor approximation to compute such limits, in french we call that a "développement limité". For example we will write sin(x)=x+o(x) with the "little-o" notation, so sin(x)/x=1+o(1) and conclude that the limit is 1.
Another example : 2sin(x)-sin(2x)= 2(x-x^3/6 + o(x^3))-(2x-(2x)^3/6+o(x^3)) = x^3+o(x^3)=x^3(1+o(1)) and x-sin(x) = x-(x-x^3/6+o(x^3)) =x^3/6 + o(x^3)=x^3/6 (1+o(1)) so [2sin(x)-sin(2x)]/[x-sin(x)] = 6+ o(1) and thus the limit as x approches 0 is 6.
I think we don't learn l'Hospital rule because it is just a particular case of Taylor approximation, and with this tool we don't have to be worry about the conditions over the limits or about g'(a) is not 0.
@@dlz5709 j’espère que ça ne te dérange pas que je répondes en français
Le développement limité se fais quasi toujours lorsque x -> 0 et fais apparaître les premières dérivées
Si tu utilises l’hôpital 1 fois tu utilises la première dérivée donc un DL d’ordre 1
2 fois 2 eme dérivée donc DL d’ordre 2
Etc ..
Can someone please explain to me why when I plug extremely small theta values into this expression on my calculator, I get an answer of Pi/180 ?
because you were using degree instead of radius.
your calculator read it as “sin(x^deg) / x “
Can you explain about d/dx (e^x) same way and how we end up with the e^x series
Could you solve it using the squeeze theorem?
One simple geometric proof is to show, on a circle, as the angle (in radians) gets smaller and smaller, the sin of theta approaches theta itself, so the limit expression is just theta/theta, cancelling out becomes 1.
What if we measure the slope of sin theta graph by joining lines and all and then relate the values with cosine theta which is too one definition of differentiation
I know practically it's not that accurate but could be done precisely
Can we use tangent method ?
How do I'll contact you?
I agree with the reason you can't use L'Hôpital, but if I define the sine function as a series just like I can define the exponential function as a series, then using Taylor Series should not be a problem since I don't need derivatives of sin. Although having said that I use the series definition of sin, L'Hôpital also becomes a viable option again.
So how would we prove that d/dx sin(x) = cos(x) using the definition of the derivative? I guess we'd use the same logic until 4:28, and then use a geometric proof to evaluate those two limits?
What if you prove it geometrically? Or is that using limits indirectly?
Finally, I understand! I have a really good book about Calculus, but I never quite understood this limit.
Is it possible to say that sin(x)/x = (sin(x)-sin(0))/(x-0) = sin'(0) = cos(0)=1 (when x goes to 0) ?
Since the limit is equivalent whether the variables in the expression and limiting variable, isn't this just a self referential equation where we can isolate the terms with "limit of sin(var)/var," factor it out, then solve for the desired limit?
I'm sorry if this question is kind of stupid but, in multivariable calculus, the directional derivative is always defined with a unitary vector, I can understand why this is necessary when doing the limit and end up multiplying by a constant, but I don't get the geometrical interpretation of getting different values of the derivative depending on the length of the vector you choose
The geometric intuition is not so far from the intuition looking at the limit which you understand. Let me walk you through:
Lets say we have a function f(x,y) and a direction vector u. As you know, the directional derivative would be defined as limh->0 f(X+hu) - f(X) / h , where the capital X is a vector that stores the point we are evaluating the derivative at. To be clear, X=(x_0,y_0) a vector.
Now geometrically we imagine a surface f, and that f(X+hu) - f(X) / h would be like a secant line analogous to single variable calculus. Where your confusion comes is that you think since h approaches zero the magnitude of u does not matter. But think again because the h on the bottom of the denominator is the same as the h on top. They are approaching zero but are the same number along the way!
So since we are dividing by h, we imagine the secant line picture and that the h corresponds to the distance between the xy coordinates of X+hu and X. Now it should be clear why u has to be a unitary vector; X+hu needs to be a distance h from X where we evaluate the function.
Additional comment: if the geometric interpretation does not click for you think about how directional derivatives are computed. Directional derivatives can be computed by taking the dot product between the gradient of the function and the direction vector. What would happen if the direction vector was only in the x-direction (u=(a,0) perhaps)? Well the dot product would only give you the partial derivative with respect to x times a. We impose the condition a=1 so that the partial derivative with respect to x is the same as the directional derivative in the x direction. We do this because it is convenient for directional derivatives to be a generalization of partial derivatives. And so we impose the condition that u is a unit vector.
@@hybmnzz2658 Thanks a lot for both comments
I love these videos!
What's wrong with SinX = X at X → 0?
Can it be anything else?
(btw is the Earth flat or round?)
Both
If I use the classical geometric definition of sin x is reasonable that L'Hôpital's doesb't the better choice. But, ¿if I use the power series definition? In some textbooks use this definition and the derivative of sin x is calculated with the derivative of a power series. Excuse me for my bad english, I'm learning English since this year.
Really like your videos ! 💙
From Myanmar 🇲🇲 (Burma)
2:30
cosh(+)
(hyperbolic cosine of plus)
Oh my cosh
I really like how for you all seems so simple :)
Are there any other exceptions to l’Hospital?
Technically this is not an exception. L'Hopitals rule does confirm limx->0 (sinx/x) = limx->0 (d/dx sinx). The theorem works, you just can not evaluate d/dx sinx.
Anyways I know what you mean though. Check out wikipedias page on Lhopitals rule and counterexamples when not following the hypothese correctly.
At 2:12 you used the sum of two angles formula right!? Well wasn't that derived from the complex definition of sine that we got from Euler's formula? And to get there we would have known the derivative of sine so that we can work out the Taylor series.
You could derive the angle addition formula by geometry 😃
It could be derived that way, but proofs for most high school students do not rely on Euler's formula.
@@blackpenredpen thanks for the info! I'll check that out
Basically every precalculus/trig book will show the sum angle rule for sine and cosine using basic geometry. The formulas are quicker found using Euler but it’s a good exercise to do it the long way. “The Limit” has more ‘funny business’ than the sum angle formulas.
Actually, if you _define_ the sine and cosine functions analyically, then their definitions are _completely_ independent of their definition using a unit circle.
Then you derive the usual properties of the sine and cosine function based on the above analytical definition of the sine and cosine function.
Didn't you make a video on this a year ago or so?
Yes, he has a video about this already
Yea, I called that “the limit” but I realized I never wrote down the part that derivative of sin(x) requires this limit thus it still caused lots of questions. This video is to show the circular reason part
What if you start by defining sin(x) as the taylor series? And then show that it got all the properties of sine. Or even better: define it as sin(x) = imag(e^(i x))
Can you also make video on geometric proof
So how to solve the initial limit?
Maybe this is just my mind as a physicist (with a love of math) but, I see no problems with using L'H rule or taylor series to DEMONSTRATE (not prove) this limit. It is a little circular but the derivative of cosine is known for all physics and engineering. Also we know L'H rule works on really messy limits that we do in physics many with ratios of trig functions (flippantly I Know). It is just from a practical standpoint easier to use L'H rule and more efficient. I appreciate the thoroughness of your statement and I would never prove this using LH rule, but to say it can't be used on expressions like that would render my work incredibly inefficient. It might be useful to clarify practical use of a rule vs definative proof of a math statement.
As a side note Demonstrating something is true should always be backed up by formal proof. I would never call using LH rule on a function like that a proof somewhere in literature. However, I'll leave that to math guys to do formal proofs of this stuff. I'm too busy doing physics work to rigorously show the limits of those kinds of functions all the time.
Perhaps amend your statement as dont us LH rule to prove sin(x)/x=1? For demonstration purposes with the asterisk to find the proof somewhere else it should be fine.
Agreed we know this limit or Taylor development and just use it. If I understand correctly he says we should not assume we know it because it involves the limit we’re looking for. Who cares ? I don’t Lol
@@Cbon-xh3ry I think this attitude mathematicians have comes from a genuine place of trying to make sure our statements are not logically inconsistant. Something I appreciate as a Theoretical Physicist. Too many physicists and engineers use the tools of math in ways they weren't intended. This would be okay if they knew what they were doing but many of them don't and that can lead to some results that don't make sense. Heck I run into this all the time when trying to define properties of fluids vs solids because definitions that seemed to be the same in one regime are different in a different regime and without careful work you end up with condricitions.
What erks me about this video it doesn't teach nuance about the mathematical toolkit one may develop. Being able to push forward even if the exact method isn't rigorous has lead me to some pretty critical insights in my research. Going through the exact mathematics is something done afterwards once I get a result and I need to prepare for a paper.
My PI has been a big advocate of making sure you are precise once you know you have a result but don't let precision weigh you down when you are trying to just make progress on a problem.
@@CrownedFalcon00 totally understand I’m just saying in this specific case it could confuse more than teach, but I could be wrong. My son’s teacher was trying to solve this and used the hôpital’s rule cause she couldn’t find the answer. They haven’t even started to work on derivatives 🤣🤣. I showed him the geometric solution but he’s not ready yet ha ha
In modern analysis goniometric functions can be rigorously defined in terms of the complex function theory and/,or through a consistent measure theory of smooth curves (as the circle is); in this way all the "familiar" analitic properties are rigorously proved without any "petition of principle".
Anyhow, the "pupil-oriented" proof in terms of arc and segment comparison of the limit sinh/h as a h tends to 0 can be evolved to a rigorous theoretical standard, because it represents the base concept of the Archimedean measurement of a circle: in the case of point you can axiomatically define the ciircle lenght as the coincident limit of two sequences, i.e. a minorant, crescent sequence of the perimeters of inscribed polygons and a majorant, decrescent sequence of the perimeters of circumscribed polygons, as the number n of sides tends to infinity. In this way, if we give this limit the traditional symbol 2pi, sin(2pi/n) and tan(2pi/n) would be defined as the side of the inscribed and circumscribed n-agon, respectively;; the equality of limits of the relevant perimeters, i.e. n sin(2pi/n)=n tan(2pi/n), both converging to 2pi, shall imply all the analitic properties. In fact, from the axiomatic definition of the circle lenghth in terms of a couple of minorant and majorant convergent sequences we get: sin (2pi/n)
sin 18° = −1±√5/4= -φ/2
Exactly why sin18° is related to golden ratio.
I don't get why it has relation or it just natural symmetry.
I think it may have something to do with being able to divide a circle into 5 equal sectors using only compass and straightedge. ( cos 72 = sin 18 if constructed - and you do have there since it only involves a square root, would give it to you 5*72=360). There must be something about the symmetry of the situation that will tell us that the golden mean (I almost wrote golden meme LOL) is happening somewhere there: there is some a and b and c there with c=a+b and b/a=c/b=phi, the golden mean.
Now that I think more, the dividing the circle by 5 and the 5 under the radical may be just coincidence.
Okay: if you draw a regular Pentagon and then connect with segments those vertices which are not already connected, you will have inscribed in the Pentagon a perfect 5 pointed star. And the ratio of the star segment lengths to the Pentagon segment lengths will be the golden mean!
@Tushar Rajput I started daydreaming about your question - see the above post.
Why not use squeeze theorem
You make very easy understand
Of course, you can always use the definition sin(z) := [e^(iz)-e^(-iz)]/2i. Then, you can use L'Hopital's rule without circular reasoning because the derivative of the complex exponential function (defined as a power series) is known.
But you need the Taylor series to prove Euler's formula.
@@oenrn Not necessarily. You can actually use just the theory of differential equations. It's not to hard to show that the function satisfying the IVP f'(x)=if(x), f(0)=1 is e^(ix) = f(x) = cos(x)+isin(x) using two elementary methods (integrating factors, and laplace transform). This proves Euler's theorem without any Taylor series.
Doesn't using Taylor series yield the right answer though? If you divide the Taylor series for sin(x) by x you get 1 - some functions of x. When you take the limit of that as x approaches 0 you just get 1. Unlike using l'hospitals rule it seems to yield the right answer.
L'ohpital also yields the right answer. The point is that you can't know the derivative of sinx until you know the limit in question. You also need the derivative for the Taylor series.
The problem is not getting the right answer. Circular reasoning is a fallacy for a different reason.
How can the limit be 1 when the smaller number is on the top in the fraction? Arc length is bigger sin. May be I ask a stupid question :-)
You can still use the squeeze theorem. Might be worth a video.
He already did here czcams.com/video/mZiPdyHyUvE/video.html
Can't we somehow compute the derivative of sinx without using the limit of sinx/x? I'm asking because I haven't yet started calculus
Joke's on you. I'm actually not using the Taylor series of the sine. Just the power series we used to define it
Can’t you mark lim y=h->0(sin h/h) and then y=bla-bla-bla +cos(theta)*y?
And then you realize that his t-shirt has the answer...
Yay, now I have a video I can share instead of going through the motions of the argument for the billionth time.
If i had any doubt, can i clarified to u??this concept is came in my studies now i understood
It was obvious from the start that that the limit is equal to the derivative of the sine function at teta equal 0, which is equal per definition to:
Lim[(sin(x)-sin(0))/(x-0)], x->0.
Now if you want to assume you don’t know the derivative of the sine function, the problem can be solved as follows:
When x 0 is x
And
Lim[sin(x)/x], x->0 is equal
Lim[x/x], x->0 which is equal 1.
You can prove the derivative is cos in many ways(geometricaly for example), you don't have to evaluate the limit in question
That doesn’t help, because that formula is how limits are defined!
Can anyone tell me difference between taylor and mclauren series
A Maclaurin Polynomial, is a special case of the Taylor Polynomial, that uses zero as our single point
We were doing exercises in class today and the teacher just told us about this, 2 hours later i watch a random youtube video from my reccomanded: do not use l'hopital on this limit
I mean this is both correct and incorrect. It cimpletely depends on your definition of sine and cosine and fortunately the most common and useful definition is to define them directly from their power series (probably as the real and imaginary parts of the complex exponential and its power series expansion). Once that's done you dont get any issues with the derivative since you can differentiate term by term. The properties of these functions that make them good for dealing with angles come as a by product. My personal favorite definition of an angle is to go through the dot product and the cosine function.
Can't you solve this using squeeze theorem?
It’s odd, since going the wrong way still gets you to the right answer. (I mean cos(0)/1 equals 1)
Yes, you will get the right answer via L'hopital.
Because in fact it is NOT a wrong way.
But it is Not Logical way at all, as the video says.
So ACTUALLY we use L'Hopital to find lim h- > 0 for (cos h - 1) / h ?