A horizontal integral?! Introduction to Lebesgue Integration
Vložit
- čas přidán 8. 07. 2020
- Support me on Patreon! / vcubingx
Join my discord server! / discord
Terry Tao's book on Measure Theory: terrytao.files.wordpress.com/...
Learn about Lebesgue Measure: www.math.ucdavis.edu/~hunter/...
More applications!
pdfs.semanticscholar.org/ff79...
Source code: github.com/vivek3141/videos
Sources: docs.google.com/document/d/16...
Follow me!
/ vcubingx
github.com/vivek3141
vcubingx.com


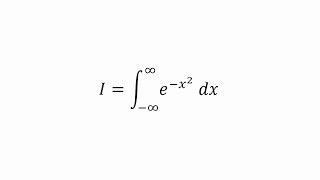






Nice one!
Thanks Grant!!
Acknowledged by the man, the myth, the legend.
He's here everybody! Shhhh! Get into your positions!
It warms my heart that Grant watched this video from a small youtuber
YES YES YES REALLY NICE ONE.
I was thinking "but can't instead I just f^-1(x) and solve for the same integral?"
But when "f(x) = constant for x in a range" it's literally impossible to do that.
And with this and the way you can apply it to probability where you can't just invert the function is brilliant!
So cool, more 3b1b inspired youtubers.. I am slightly jealous of kids today who are getting this level of education for almost free.
The day may come when you can download knowledge onto your brain like a computer. I'm not sure how universally jealous people would be of that though lol
one of the best things to happen to this world since 1940
I had to figure EVERYTHING out on my own!! I had a textbook and professors that tenure and were pissed about the number of courses they had to “teach”.
Yet many kids out there spend tons of hours watching TikTok dances
Yes, learning resources are more prevalent and easily accessible, but so are distractions imo
Great video Vivek! =)
Thanks Papa
Now I am waiting for some cursed meme about factoring f(x) and integrating Lebesgue Integeral with respect to miu.
Papa is here too omg
@@vcubingx is he your father?
@@Sciencedoneright his name is papa
As the King of Calculus, Riemann, faced the Dirichlet function, Riemann asked the function, “Are you Riemann integrable because you are continuous? Or are you continuous because you are Riemann integrable?” (note: this iff statement is not actually true) Riemann began to open his domain *”Malevolent Shrine”* and *cleaved* the area under the curve into slices approaching infinity. However, the Dirichlet function is continuous nowhere, and by *contradiction* the function simply stated “Stand proud. You're strong but Nah, I’d win.” Bernhard Riemann’s domain crumbled. In his dying moments, Riemann uttered the phrase “With this treasure, I summon…” Because in sets of measure zero always bet on *Lebesgue.* The proof was trivially concluded, and those who pioneered the techniques of calculus, the ones who formalised the integral, they would all bear witness to the one who is free. To the one who left it all behind, and his overwhelming *integrability!*
Clciked and thought it was 3b1b, glad I made that mistake, great video!
At 7:19, E(x) should be the integral of x*P(x), not just P(x). The integral of P(x) is 1!
Yes and he should have written f(x) or something else, P(x) suggests probability but it's the density what he is plotting and is used to compute expectations. Amazing that the author hasn't pinned your comment yet
Exactly right!
Yes
@@Pabloparsil Exactly but it remains a confusion between x the variable of integration and X the random variable. I would have written E[X] = integration of x *f(x) dx (f the density) or integration of x dP(x) with P the measure of the law of X (don't know of to say it properly sorry)
This is excellent. Every time I've tried to understand lebesgue integration in the past it was presented as something complicated and hard to understand, but you've made it so simple. I'm sure there's more detail you didn't cover, since once video can only do so much, but you've actually given some good intuition what what a lebesgue integral actual IS, which is something I haven't been able to find in any of the many other explanations I've found. Thank you very much!
These animations just look so good :)
Thank you so much! Your videos were incredibly useful when I was learning this topic.
@@vcubingx Thanks. Glad I could help :)
@@vcubingx weak sauce.....not enough examples & theory....
i follow both of the channels and man this feels very nice of everyone coming together and learning the topic so nicely. I really love the way you have presented lesbegue integral... I need to watch it more times for sure to get a little more understanding, but this is feels so nice!
just switching how you construct rectangles to find area can do so much... would have never imagined that...
This is so cool for sure. Animated presentation is really good
One thing I'll give as an advice : don't stop. I looked back at myself from after 6 years and I'm ashamed of how better I was at 14/15/16/17. You're at an awesome level. Make sure it's not your peak!
Awesome video :)
What field of maths did you learn at that age when you were younger so I can compare with myself. I feel like I'm learning too slowly to ever accomplish anything..
Good video! You have an amazing talent of effectively illustrating complex ideas in a simple manner. Keep up the good work!!
Thank you very much!
Please do more of these vidoes! Good explanation. Would love some intuative measure theory / functional analysis.
Superb!!!!!
This video just inspired me to extend this result into a deep area of number theory!
7:25
Isn't it supposed to be the integral of
x p(x) dx
For the expected value function yes. The integral in the video sums to 1
I think it is P(X) = x*f(x), with f being the PDF.
Mehmet M Mehmet M if that is the case that would be an unusual way of notating that. Usually the Probability = ∫ PDF(x)dx. In this case his P(x) is his PDF. The integral for E should be of E = ∫ x p(x) dx
@@stefanjenkins6196 I know, that this was a typo. But nevertheless, I appreciate your nice explanation.
This comment should be on the top pinned. I hate that the corrections always get buried under the fangirl comments. We get it... It's a great video. Can we get to scientific content distribution 2.0 already where this problem is sorted?
This channel deserves much more subscribers than it has now
So much better than my Lebesgue Integration Course!!!
Can't wait to see how your content grows! Thanks for the video.
Thanks Aaron!
Mate I have an lesbegue integration exam in a few hours and was nearly having a panic attack till this video came along, thanks so much! Subscribed!
This channel is gonna explode. Thanks for the explanation.
Vivek my man !
Ur killing it with those animations !!! 🙌
Great video! Lot of thanks for clarifying a frightening concept
The "limits of rectangles" explanation is what they teach you in high school calc, is how Newton/Leibniz thought of integration, and is correct to a good approximation, but it's not technically what a Riemann Integral is. Riemann Integrals (which are taught as a rigorous framework in Real Analysis class) are actually more powerful, and are able to integrate any function which is continuous "almost everywhere".
-----------
Take Tomae's Function, which is extremely similar to Dirichlet's Function that you showed:
f(x) = 0 if x is irrational, 1/n if x = m/n (rational)
This function has infinite discontinuities. However, it's discontinuous at every rational number and continuous at every irrational number(!!). Since there are only countably-many discontinuities, it's continuous "almost everywhere" and is therefore Riemann Integrable!
-----------
In fact, it was discovered in the 50's that a small tweak to the definition of Riemann Integrals makes them strictly stronger than Lebesgue Integrals - that is, every function which can be integrated using Lebesgue's Method can also be integrated using these new "Generalized Riemann Integrals", but the converse is not true!
damn, i shouldn't have taken up engineering.
This one, right?
en.wikipedia.org/wiki/Henstock-Kurzweil_integral
@@xCorvus7x Yes, that's the Generalized Riemann Integral.
@@BlueRaja *Riemann integrals are actually more powerful, and are able to integrate any function which is continuous "almost everywhere".*
This is incorrect. There is only one Riemann integral, and the Riemann integral cannot integrate the indicator function of the rational numbers embedded in the real numbers, even though this function is bounded and continuous almost everywhere. In fact, this is one notable point of weakness of the Riemann integral that led to the development of the Lebesgue integral in the first place. Also, the claim that the Riemann integral is more powerful is just false. A well-known theorem of real analysis is that a function f : I -> R is Darboux integrable if and only if it is Riemann integrable.
*Yes, that's the generalized Riemann integral.*
Calling it this is misleading and incorrect, as this is not the name of the integral. Yes, the gauge integral is a direct generalization of the Riemann integral, but it is not called the generalized Riemann integral. Also, one important detail you neglect is that the gauge integral is only a stronger integral when we limit ourselves to functions in R^I. The measure-theoretic framework for the Lebesgue integral is more robust in that one can perform integration on arbitrary measurable spaces (X, Σ), rather than just (R, B(R)), which is the space in which the gauge integral is defined on.
A more in-depth exploration of the subject reveals that the direction in which one generalizes from Riemann integration to measure-theoretic integration is a different one than the direction in which one generalizes from Riemann integration to gauge integration. It is possible to produce a tweak like the one from Riemann integration to gauge integration whilst simultaneously applying the Lebesgue framework of generalization of spaces. This shows that while the gauge integral is better behaved, it is not a broadening of scope in the same way Lebesgue's framework is.
@@angelmendez-rivera351 The "Generalized Riemann Integral" is the name we learned for it in Real Analysis class, and also the name my Real Analysis textbook uses ("Introduction to Real Analysis", Bartle+Sherbert, 1999), and is one of the names listed on the Wikipedia page. So I feel pretty confident in saying I'm not incorrect in calling it that.
That same textbook also has this:
Theorem 7.3.12 "Lebesgue's Integrability Criterion": A bounded function f : [a,b] → ℝ is Riemann Integrable if and only if it is continuous almost everywhere on [a,b]
So I feel pretty confident about that claim, too. Your mistake is that "the indicator function of the rational numbers embedded in the reals", aka. Dirichlet's Function, is continuous nowhere (see en.wikipedia.org/wiki/Dirichlet_function#Topological_properties for a proof)
---
When I said "Riemann Integrals are more powerful", I meant "more powerful than the limits of rectangles explanation would imply". Not "more powerful than Lebesgue integrals"
This channel has so nice quality! Congrats! :)
Thank you so much!
Very nice explanation, it has been awhile since I took a measure theory class so my memory of it has diminished, but your explanation perfectly encapsulates the main concept behind Lebesgue integration.
Where textbook lag; you proceed with your animation and make sense what the hell mathematics underneath which is very appealing to visualize absurd abstract idea from where concept are taken. Nice work bro; mathematics channel like you are life saver for viewer.
3:14 this is a bit too quick. While the probability for this one number is 0, we also have an infinite amount of other rational numbers it can be. So the total probability is an infinite sum of things. To determine that that is 0 you need some more arguments.
Came to same this
This video is worth watching.... I really liked the way you described lebesgue integral really learnt something interesting subscribed ❤
Beautiful explanation! Thanks so much for this video :)
Glad you enjoyed it!
Your English has gotten very good!
Thanks, I'm very happy with my improvement too
You're talented my dude, keep it up.
You make such amazing videos 🙌
Very clearly explained! Congrats!
Thanks a lot!
I really like the analogy to expected value. It's much more helpful than the coin analogy in Lebesgue's quote. The coin thing is too vague, but expected value is much more specific and so is a much more satisfying analogy.
I also really appreciate that you gave a specific real world example of when Lebesgue integration would be useful. Personally, I particularly like the example with circuits as I'm an Electrical Engineering major.
Glad it was helpful! Thanks for watching!
@@vcubingx Thanks for making the video. 3b1b linked to it on his patreon and said it had similar animations to his videos. When I saw it was on Lebesgue integration I was excited, as every other explanation I'd found on the topic was too technical. A video similar in style to 3b1b that explained it sounded right up my alley and it was. I also watched your video on fractional calculus which was pretty interesting too.
Thanks, and it's so easy & simple!
Nice explanation, will looking forward for other technique from you. 😀
Ayanokoji learned this as a 5 year old
Reason why I came here bro Ayanokoji is just HIM.
Excellent video lecture.
Easy to understand! Thank you!
Very nicely explained!!!
Damn this video was hot!!!!! Pure flame xD i never understood lebesque integral since I'm an engineer and you explained it in such a perfect way 👌🏻 hope you become an university profesor one day :)
THANK YOU SO MUCH FOR THIS! Now I can learn the difference between classic reimann integration and this technique.
Glad it was helpful!
7:15 shouldn’t it be the integral of P(x)*x?
The idea that somehow the Lebesgue integral is "done horizontally" is misleading.
The Lebesgue integral is defined _exactly_ like the Riemann integral, except that for the Lebesgue integral the simple functions are linear combinations of characteristic functions of _measurable_ sets rather than just intervals.
Then, once you've defined it, you prove that the integral is the area of the subgraph, you prove Fubini's theorem, and the "Cavalieri principle": all this allows you to rewrite the integral "horizontally" so to speak.
No need to directly define the Lebesgue integral "horizontally".
This was amazing to watch 😊
thankyou, that was a very clear explanation
I didn't understand anything but the visuals are amazing. Great job!
Great videos! You have my subscription.
Great video! I encourage you to go on
Great video!
Hey, nice video! Clear presentation 👌
If I may, can you skip less steps? Since it's a new concept for the viewer, it would help if you go slower even if you are using an argument you already went over earlier. It would help if you repeat the logic of the argument again while using it, just for clarity and connectedness.
I just discovered your channel and Im excited to look at the rest of the videos! Keep goingg!! 👌👍
Thanks for the feedback! I'll definitely keep this in mind when I make my next video!
Great video mate
Thanks!
excellent video.
1:01 Not to ruin what is an otherwise perfect video but continuity has a typo
Good catch! I'll see what I can do about it.
Yep. THere's an extra i the way he spelled it.
Is the Graph at 6:50 correct? I'm not very deep into the mechanics, but as far as I understood the y_i * mu(A_i) is rectangle below the measurable Function similar to Rieman, but instead of equal x-length for the dx intervals the x-length is determined by dmu intervals on the y-axis. Please correct me if I am wrong.
and it get paid out in the currency that somebody get some new knowledge, simply you get our satisfaction of knowing something, thank you, it is good, correct and sustainable.
Thanks for the video
Good job!
Thanks so much for this :)
You are the 3Blue1Brown.Jr great video.... !!!
😂 I thought it was him when I clicked on the video
This is the best video 👍👍...Please sir give us more video about this topic and give us more example...
very lovelly explanation
Great video
Nice , very nice . Please which App did you use for the graphic visualization of those area
Waiting for your next video brother
The sources are awesome, I couldn't understand wikipedia but with "(Riemann) Integration Sucks!!!" from Peyam i could understand a lot more. Good video
i keep seeing this vid's thumbnail and thinking it says "lesbian integrals". hats off for finding a way to stick out in my mind. youve earned my view
Heyo ! Thanks for the vid, it's great :) what's your outro music btw ?
Excellent!
I think the explanation will be even clearer if you mentioned more on what 'Lebesgue measure' is, at 5:07. Other than that great work!
I agree! Watching it back I realized that I skimmed over the idea of the Lebesgue measure, but it's definitely an incredibly important topic.
@@vcubingx Maybe you can make another video on that topic. I think Tao's book did a good job of explaining it. (Chp 1.1 to 1.3 I think, I am learning this myself now too) An animated version of that will be fantastic!
@@rzhang3927 I'll look into it! Definitely a fantastic idea.
Thank you brother
This method is also the best way to integrate a normal distribution put into the 3rd dimension using multiplicative integrals but to do that it’s almost ALWAYS just 2 of them.
After looking at a couple of your videos I wondered, do you use 3b1b's manim python library for your animations?
I'm very sure he does... although you would have discovered it by now...
Sir ! Which software did you use to make these awasome videos.
whoa ! this is so cool :O which book/site are you referring here?
If you take an increasing sequence of Riemann integrable functions, the limit might not be Riemann integrable. And even if you happen to know the limit is Riemann integrable, it is still very tedious to prove that the limit of the integrals is the integral of the limit (a result, which seems obvious). With Lebesgue integrand this is almost trivial to prove. Historically this was very important.
Another main motivation historically was Fubini's Theorem. There the Riemann integral is again in trouble with "integrability issues" . With Lebesgue integral Fubini is a breeze really.
Cool.. Got to learn something new...
Please make a comparison video of reimann vs lebesgue integral, for the same calculation..
Nice video
Thank you for this ... 🥰
Are you planning to take real/complex analysis in high school? You're still in your junior year right? I think you'll have plenty of time! Btw, did 3b1b's probability series inspire you to do this video on Lebesgue integrals or was it just your own curiosity? Your videos are awesome, keep up the great work!
I don't think I will. The college I take my math courses at right now doesn't have an analysis course.
Thank you for this video! What about visualization of Ito Integral in contrast to Riemann/Lebesgue Integration please?
Glad you liked it! That's a tough topic to cover, so probably not anytime soon
At 7:38, the verbal emphasis on $5 is the same as that on $10, so (listening, not watching closely) I got confused in the subsequent math and had to back up to see what I'd missed. Not a complaint, just a note that inflection is relied upon by at least one viewer :). Thanks for the video!
Dude, you are the god of animations. Lebesgue might be cool, but your animations are cooler.
Maybe, you animate Itô the next time. :)
great explanation! very cool
hackerman
lol
will u tell me the software that u use to make these animations?
god bless you omg I finally understand this
The original idea of Lebesgue integral is the measure of the area under the graph which is later discovered to be coincided with sup of integrals of simple functions
Thank you sir i have problem on language but I can understand
Your explanation is good i give 2 subscriber and without skipping add this is small contribution for you by me
❣️ Keep making such as amazing video
Sir are you making the video on manifold
I think you haven't understood the Lebesgue integral at all. The animation with horizontal rectangles is quite flawed. That's not how it works!! Rectangles are vertical, what happens is that we split the range of the image into different sections. In each of them, we take an arbitrary point, and multiply it by the inverse function of the section. That may be one or more VERTICAL rectangles.
I remember this when we studied Cantor sets
Awesome!
To Visualize 4D object, think blue cube, split in half, and the second half is color coded sides that represent each cube value in a color.
Doesn't make sense
Faulty reasoning, truth is we have no conceivable idea of what the 4th dimension would be, just like a 2D being can't conceive what the 3th dimension is, purely our assumptions that are probably wrong
Thank you.
Aaaahhh yes. I remember these
It's me 3 years later!
Thank you
I don’t like your 0.123123... It could be 0.12312345645612312345645600000...Rational but not matching your decimal string in the nth place. Still, you’re right of course that the integral is one, and if you switch to f(x)=1 if x is rational and 0 if x is irrational, the integral is 0. The rationals form an everywhere dense set of measure 0 on the interval.
loved it .
can you make a step by step solution to some Lebesgue Integral?
This video is great. But you teased im the beginning with 3 and 4 dimensional volume problems. So I was expecting a follow up on why Lebesgue integration is more natural or intuitive in that setting. Do you plan on a follow up?
If not, you may want to look for some video on Lebesgue measure in R^n.
I love you mann!!!
Overall a good video, though I have a few comments.
The figure featuring horizontal slabs on your thumbnail does not actually describe the Lebesgue integral. That figure indicates that we sum slabs of a fixed height and varying widths to approximate an integral. This is not accurate, as you describe yourself in your video. What happens instead is that we decompose the image of the function into a partition of intervals. The low end points of these intervals will be our weights for approximating an integral. We then collect the preimages of those intervals, which may be disconnected sets. However, these preimages will be measurable (by, e.g., continuity of the function. More generally by measurability of the function.) We then multiply the weights by measure of the preimages. In the coin counting analogy, the function values (which I'm calling weights) are the "number of coins of each type" and the measures of the preimages are the "values labeled on each coin."
Also, I don't believe that the step function example is a good explanation as to why the Riemann integral is not preferable. There isn't any concern of mismatching upper & lower approximating sums in this case. Showing a visual of a more clear refinement demonstrates this. The problem with partitioning domains in high dimensional space is a good reason, but it isn't due to some conceptual complexity with domain decomposition. It is more that proofs on the properties of the multivariate Riemann integral require rather laborious notational baggage from multi-indexing high dimensional boxes combined with a time spent concerning the reader with the definition of measure zero sets while not actually trying to teach measure theory. Best reason to care about Lebesgue is going to be the use limiting properties, e.g. dominated convergence theorem.