The Integral of 1/x EXPLAINED. It's NOT what you think...
Vložit
- čas přidán 24. 10. 2020
- Learn how to find the Integral or Antiderivative of 1/x. Unfortunately, you can't use the traditional power rule for integrals to solve this. Even if you remembered the derivative of the natural log of x, ln(x), is 1/x, you wouldn't have the complete answer! Watch this video to find out the solution!
For more help, visit: theacetutors.com
For more videos/content, visit: theacetutors.com/blog
Sign up for tutoring: theacetutors.com/register



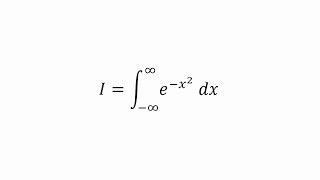





Great, I already knew that. This does nothing to explain why it is what it is.
Here's why it is what it is.
Suppose we are allowed to use the following as building blocks to get the answer:
1. The power rule, in both directions
2. Exponent properties, such as the change-of-base rule
3. The derivatives of exponentials
4. L'Hospital's rule and limits
Let h be a number arbitrarily close to zero. This means 1/x is very close to x^(h - 1). Integrate with the power rule and get:
1/h*x^h + C
Let the arbitrary constant be -1/h:
1/h*x^h - 1/h
Consolidate as a single fraction:
(x^h - 1)/h
Take the limit as h approaches zero. We get an indeterminate form, so use L'H's rule:
d/dh x^h - 1 = d/dh e^(ln(x)*h) - 1 = ln(x)*e^(ln(x)*h).
Evaluate at h=0, and get: ln(x)*e^0 = ln(x)
d/dh h = 1
L'H rule result:
limit 1/h*x^h - 1/h as h goes to zero = ln(x)
You are a very kind person to have written all that out. @@carultch
The funny thing is that the power rule works fine for values of n very close to -1. If we graph the antiderivatives for F(x) = (x^(n+1) -1) / (n+1), then as n -> -1, the graph will approach G(x) = ln x.
In this case the constant of integration matters: C = -1 / (n+1) .
very helpful! thank you!
Thanks for the explanation
You are very very welcome! Thanks for watching!
thankyou so much for the explanation
You are so so welcome!
It's funny that the thought of dividing by 0 makes you sick 🤣
I don't even want to think about it hahahah
Is there a more thorough proof aswell?
There definitely is, however, for this video, I tried to stick to the high-level concept instead of the in-depth proof.
integral of 1/x ≠ lnx + c
integral of 1/x = ln|x| + c
Excuse me, is this Mark from Ace tutors? You didn't introduce yourself in the beginning :(
Hahahaha! I'm so sorry for the confusion! It won't happen again!
I thought you would explain why your result is incorrect.
If you ask what's the indefinite integral (i.e. the family of all the antiderivatives) of 1/x in any interval where it's defined, the answer would be ln(|x|)+c.
Instead, the correct solution, the family of all the antiderivatives of 1/x, is the following:
ln(x)+a for x>0 and ln(-x)+b for x
In the complex world, the log of any complex number (z) is ln|z| + i*[angle(z) + 2*pi*k], where k is any arbitrary integer. You can derive this by letting e^L = |z| * e^[i*angle(z)], and solving for L. This explains where the absolute value comes from, and how it is consistent with the bigger picture. Simply let our constant of integration be real for positive real inputs, and imaginary to cancel the imaginary component, i*(pi + 2*pi*k), and you salvage the Calc 1 level solution.
Most introductory calc teachers keep it simple and just add +C to ln|x| and call it good enough for first year students. You can't evaluate it directly across the singularity at x=0 anyway, so it is very rare that the dissimilar constants of integration ever matter in a problem.
You can integrate 1/z around the singularity in the complex world, to evaluate it across two real numbers of opposite signs, and you'll have a path-dependent solution. This is because the result will depend on how many rotations you took around the singularity, as is reflected in the arbitrary integer of k.
this was exactly what I thought
why does power rule work for every power except -1, like i get that when u put it in the formula it doesnt work, but conceptually what is special about the power being -1?
To use the power rule on negative 1 means you must divide by zero, so it is mathematically illegal. Just like how 1/x has domain everywhere except 0, the power rule works everywhere except -1
@@MULI-ul1is Mathematically illegal 😆😆that's so accurate though
There is a way to connect the integral of 1/x, to the general power rule.
Consider the integral of x^(h - 1) dx, where h is an arbitrary number, very close to zero. The integration power rule will give us:
1/h * x^h + C
For the constant of integration C, all that matters is that it is NOT a function of x specifically. It is OK for it to be a function of h. In fact, strategically letting C = -1/h, will get us where we need to go.
1/h * x^h - 1/h
Regroup it, as a single fraction:
(x^h - 1)/h
Observe that in the limit when h goes to zero, and x remains a positive number, that x^h approaches 1. This gives us an indeterminate form, of 0/0, which allows us to use L'H rule to reconcile the limit. Let N = x^h - 1, and D = h.
dD/dh = 1
For dN/dh, rewrite the exponent term in base e:
x^h = e^(ln(x)*h)
dN/dh = ln(x)*e^(ln(x)*h)
Thus, for L'H rule:
[dN/dh]/[dD/dh] = ln(x)*e^(ln(x)*h)
Now all we have left that depends on h, is e^(ln(x)*h). Take the limit as h goes to zero, and this becomes 1. We're left with ln(x).
So sure enough, this problem point for integrating 1/x with the power rule, turns out to converge to ln(x) after all, when approaching it with the power rule.
What happens when the integral has a coefficient?
Great question! If the function in the integral has a coefficient, you can actually take that out of the integral and multiply it to your solution in the end! I hope this helps
@@AceTutors1thank u sir
Where does C come from. I'm so confused
Great question! Zayden provided an awesome answer to this. It's just a placeholder for the potential of there being some constant number in the function
@@AceTutors1 awesome! Thank you so much, this actually clears up quite a bit!