The fundamental group of the circle

This is the second video for the course Topologie en Meetkunde taught in Utrecht University. We introduce the fundamental group, and we compute it in the case of the real line and the circle.
Once you watch the video, try to answer the following question: How would you endow the fundamental group with its group structure? (Attempt first to see what is going on in the case of the circle!).
00:00 Recap
01:52 Statement of the results
02:48 The real line
05:00 Euclidean space is contractible
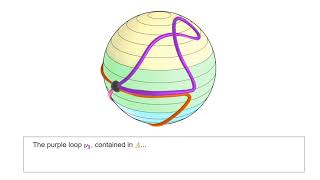
05:22 Loops in the circle
06:32 The real line covers the circle
07:55 Lifting paths
11:06 Homotopies
12:54 Summary
Website of the Utrecht Geometry Centre: utrechtgeometrycentre.nl/
Lecturer: Álvaro del Pino (alvarodelpino.com/)

[@tim-701cca]

It is so great to see a visual proof like that!

[@documentemail7299]

Can you make so many videos like this. this kind of visualization is really needed in algebraic topology...

[@EugenieBeaublanc-sf9wg]

these are so cute I cant believe I didnt know you existed.

[@forheuristiclifeksh7836]

4:27

[@Khashayarissi-ob4yj]

so excellent, so beautiful
With regards

[@KaliFissure]

Surface(cos(u/2)cos(v),cos(u/2)sin(v),sin(u)),u,0,2pi,v,0,2pi
Notice that 4pi are needed to complete the surface.
This is because this is a single sided surface.
The radially symmetric Klein bottle.
Not a torus.

[@pritamroy3766]

Please tell me the difference between homotopy and homeomorphic, im very much confused about these two terms.

[@lorenzobarbato4558]

In topology, the objects are topological spaces and the morphisms between them are continuous maps (i.e. the maps that interact well with the structure one is interested in in that case). The 'best' kind of continuous map is a homeomorphism: homeomorphic spaces are essentially the same objects through the lenses of topology (i don't mean that they are really the same object, but that they have really the same topological properties. It's the analogous of a linear isomorphism in the case of vector spaces). Anothet concept is the one of homotopy equivalent spaces. This is a weaker notion, that however preserves a lot of good invariants one is usually interested in (for example in algebraic topology). Essentially, two spaces are homotopy equivalent if one can be continuously deformed to the other (this is just an intuition. Of course it must be taken with a grain of salt). It is indeed a weaker notion: there are homotopy equivalent spaces that are not homeomorphic. Think about an open ball in the plane, that can be deformed to its center by sliding radially. These two spaces are certainly homotopic, but not homeomorphic (if you want, they have different dimensions as manifolds, but one doesn't need such a big cannon to see this. It's enough to notice that there's not a bijection between an open ball in the plane and a point: but a homeomorphism is in particular bijective)