
- 20
- 26 426
Katherine Kelm
Registrace 3. 09. 2017
Arc Length and the One Half Trick
Explanation and examples of the "one-half trick", a special case of functions for which the integrand for the arc length can be simplified and evaluated.
zhlédnutí: 18
Video
Tricky arc length examples
zhlédnutí 36Před měsícem
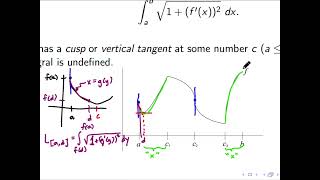
Finding the length of a curve f on [a,b] that has a cusp or vertical tangent at some number c between x=a and x=b. Includes graphical and analytical examples.
Area between curves
zhlédnutí 31Před měsícem
Using slicing and the definite integral to derive a formula for the area between two curves. Includes examples.
Slicing and the Definite Integral
zhlédnutí 32Před 2 měsíci
Introduction to the concept of slicing as a tool for setting up definite integrals to compute area, volume, arc length, work, and hydrostatic force. Includes several examples and a concept check. Intended for students in Calculus 2 (AP Calculus BC).
Gradescope tutorial video
zhlédnutí 235Před 2 lety
Tutorial showing how to upload an assignment to Gradescope, assign pages, and add group members.
Order of an Element of a Group
zhlédnutí 664Před 2 lety
Definition of the order of an element of a group. We prove several basic results concerning the order of an element of a group, and work several examples and concept checks.
Abelian Groups
zhlédnutí 815Před 2 lety
Definition, examples, and non-examples of abelian groups, with concept checks. We assume familiarity with the definition and basic properties of groups; integers modulo n, matrices, and Bézout's Lemma.
Polynomial Congruence
zhlédnutí 821Před 3 lety
Review how the ring of integers is similar to the ring of polynomials in x over a field F; construct the quotient ring of polynomials modulo the ideal generated by a polynomial; show how this quotient ring is similar to Z_n; and work a few examples and concept checks. We assume familiarity with the definitions and basic properties of the ring of integers; quotient rings; principal ideals; and p...
Ring Homomorphisms
zhlédnutí 344Před 3 lety
Definition of ring homomorphism and ring isomorphism, review of basic properties. Includes several examples. Replaces older video.
Rational Root Theorem, with Proof
zhlédnutí 1,3KPřed 3 lety
Rational Root Theorem, aka Rational Zeros Theorem, with proof, examples, and concept checks.
GCD of Two Polynomials over a Finite Field
zhlédnutí 13KPřed 3 lety
Definition of the greatest common divisor of two polynomials over a field F as the unique monic polynomial of greatest degree that divides both polynomials. Demonstration of how to use the Euclidean Algorithm to compute the gcd of two polynomials over a finite field, and to find a linear combination of the two polynomials that equals the gcd. Includes examples and concept checks.
Kernels, Homomorphisms, and the Natural Projection Function
zhlédnutí 262Před 3 lety
We explore the relationship between the normal subgroups of a group G and the group homomorphisms on G induced by the natural projection function. Includes worked examples and concept checks.
Correspondence Theorem for Groups
zhlédnutí 2,7KPřed 3 lety
Statement and proof of the correspondence theorem for groups, with examples and concept checks.
Classification of Groups of Small Order
zhlédnutí 821Před 3 lety
Classification of groups of order less than 12. Intended for students of undergraduate abstract algebra. Includes concept checks.
De Moivre's Theorem and Roots of Unity
zhlédnutí 630Před 3 lety
A review of the polar form of a complex number; De Moivre's Theorem; roots of unity; primitive roots of unity; examples; concept checks.
The Group of Symmetries of an Equilateral Triangle
zhlédnutí 1,1KPřed 3 lety
The Group of Symmetries of an Equilateral Triangle
Greatest Common Divisor of Two Polynomials Over a Field
zhlédnutí 806Před 5 lety
Greatest Common Divisor of Two Polynomials Over a Field








Thank you so much mam.🙏🙏
Well thought outyou should post more!
22:30 Hydrostatic force example
Thank you! Most understandable worked examples I've seen.
Thanks for sharing ma❤❤❤, it really help me in school. Thanks once again
5:00 Second result should be the matrix [ 1 1 \\ -2 0 ] rather than [ 1 1 \\ -2 1 ].
Ring Theory exam in 4 hours and polynomials is yhe last thing left to understand. I've been failing to get this. Finally understand. Thank you so much for this video 🙏
Good 😊
Very neat, clear and thorough, and answered many of my questions. Thank you so much. 🙏🙏🙏🙏🙏🙏
A very great proof. Thank you for this ! Keep your good work coming :)
I really appreciate such content.....
Best video ever. Thank you SO MUCH.
So, two questions about the slide at 3:00 . 1. Possible typo: Isn't (x^3+2x^2+1)/(x+1) = x^2+x-1 ? 2. Why was x+1 multiplied by 2 in x+1 = (2x+2)*2 ? Was it to somehow get no remainder after the last calculation? Wouldn't 2(2x+2) = 4x+4 ? I feel like I'm missing something...
1. All coefficients are taken modulo 3, so x^2 + x - 1 is equal to x^2 + x + 2. 2. Yes. Again, 4x+4 = x+1 over Z_3.
@@katherinekelm7439 Right! Thank you! I missed the Z_3, I'm unused to finishing with a modulo...
@@katherinekelm7439 So what would happen if we had a polynomial like 3x+3 over Z_3, would it all turn into 0 since 3 mod 3 = 0 or x+1 ?
@@pedromendes6846 Yes, the coefficients are actually congruence classes in Z_3, so 3x+3 is actually [3]x+[3] = [0]x+[0].
9:04 Pause and Explore example should read 10x^3 - x^2 - 17x - 6.
20:39 Small typo in last line; right hand side of the equation should say 4x(3x+1) + 0.
Thank you so much, Katherine! All your videos are just fantastic. I immediately subscribed to your channel.
Is it safe to say that the set of all linear (integral) combinations of a and b, represented by ax + by is the same as the set of all multiples of gcd(a,b). { u | u = ax + by, x,y are integers } = { v| v = k* gcd(a,b), k is an integer }
Yes. Every linear combination of a and b is a multiple of gcd(a,b), and every multiple of gcd(a,b) can be written as a linear combination of a and b.
@@katherinekelm7439 I am going to use this set result to produce a corollary. Note that i will use (a,b) in place of gcd(a,b) for readability. So to recap , given integers a,b not both zero and defining the sets A and B , A = { u | u = ax + by, x and y are integers } , B = { v | v = k* (a,b) , k is an integer }, we can prove A = B , using two set inclusions ( i will not attempt that but it can be shown). We immediately get the following corollary, for integers a,b not both zero, "Given integers x,y such that ax + by = 1, it follows (a,b) = 1" Proof: By the set equality, we get ax + by = k * (a,b) for some integer k . Since we are given ax + by = 1 , by substitution 1 = k * (a,b) . but (a,b) >= 1 since a,b are not both zero, whence it follows that k must be 1. (I think this makes sense, since k is an integer and the only way to factor 1 into a pair of integers is 1*1 or (-1)*(-1) ). Thus (a,b) = 1. Maybe this is not the customary presentation of this number theory result, or the most efficient, but i do like the set theory flavor , and the logic is transparent. Sorry if this seems pedantic, it feels more amenable to numerical exploration ; i can open a maple document and experiment with such results, comparing sets. As some mathematician once said, all of math can be reduced to sets.
@11:11 I believe the proof for pt.2 should be xN yN (xN)^-1 and then we have normality of cosets. Great video!
Quite right. Good catch!
Thank you so much, Katherine! Your video is a piece of gold, so helpful!
Great work. May I know which screen recording application you are using
This video was created using Camtasia.
@@katherinekelm7439 Thank you
Wrong in 0:00 Zn is not equal Z/nZ, only are isomorphims
It depends on how one defines Z_n. In most books Z_n is defined as the set of all congruence classes (mod n). So the class [k] in Z_n is exactly the coset k + nZ in Z/(nZ).
Nice explanation Ma'am .Your animations is exceptionally neat and lucid to understand.Do make more videos on Mathematics.....
Thank you, you have helped me a lot.
czcams.com/video/Ya7IcuR0bEQ/video.html
What will be gcd of X²+3 and X³+6X+1 in Z_7? Please answer with explanation.
If you use the Euclidean Algorithm to divide x³+6x+1 by x²+3, the last non-zero remainder is 3x+1. Factoring out 3, we get 3(x+5), so the gcd is x+5. You can check that x³+6x+1 = (x+5)(x² + 2x + 3) and x²+3 = (x+5)(x+2).
Thanks
Thank You! I found it helpful
Awesome 😍💋 💝💖♥️❤️
Thanks! So when we write out a polynomial in F[x] as the linear combination of powers of some 'x', what exactly is this 'x' here? Is it also part of the field F?
The 'x' is considered "indeterminate", meaning it is just a place-holder and not an element of any field. F[x], then, is just a collection of objects called "polynomials" that just happens to have a ring structure when we add and multiply the polynomials in the usual way. There are some results that allow us to "plug in" field elements for x and get something meaningful -- for example, we can talk of a "root" of a polynomial f(x) which is an element c of F (or of an extension field of F) such that f(c) = 0 -- but the basic ring structure of F[x] is independent of such results. Hope that helps!
Ah I see, thanks for the detailed response! So it seems that these polynomials aren't really functions, huh. What might be the rigorous way to construct a function out of a given polynomial? What are possible options for what the domain of the function could be? (since there needs to be a notion of "multiplying x by a coefficient, or taking powers of it")
@@aditya_a If F is a field then you can always create a function f: F → F defined by a → f(a), where f(x) is a polynomial in F[x] -- in fact you could use f : K → K where K is an extension field of F, i.e. a field where it makes sense to add and multiply elements of F. For example, consider f(x) = x^2 - 2 with coefficients considered to be rational numbers. Let f : R → R (R = the set of real numbers) be defined by a → a^2 - 2 for each a in R. Since every rational number is also a real number, this is a well-defined function.
9:58 I misspoke; I meant to say that c is the gcd of a-b and b.