Video

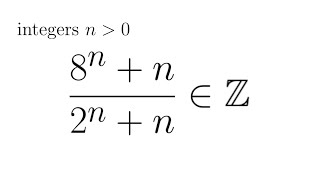
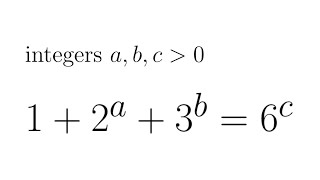
nice

This is a little bit hard for a 1987 P4, but I have a different approach than this

No sol

Nice problem!

K I liked your solution very much

The Pythagorean triple part was very well thought out.

Bro change the background screen black. It will be good for our eyes

2009=7²41 √a=√(2009) - √b a=2009+b-2√(2009b) but a is an integer so √(2009b) = 7√(41b) is an integer so b=y²41, similarly (symmetry) a=x²41 original eqn => x√41 + y√41 =7√41 x + y = 7 so x runs from 0 to 1 as y runs from 7 to zero thus solutions (of the form n²41) are ... 0,2009 41,1476 164,1025 369,656 656,369 1025,164 1476,41 2009,0

Why not provide proof problems ?

Hi can u tell me how approxh to solve putnam problam

I have a simpler solution: assume such f(x) exist if f(x) < x + 1987 / 2 f(f(x)) < f(x) + 1987 / 2 < (x + 1987 / 2) + 1987 / 2 = x + 1987, conflict with f(f(x)) = x + 1987 so f(x) >= x + 1987 / 2 , this is conclusion 1 if f(x) > x + 1987 / 2 f(f(x)) > f(x) + 1987 / 2 > (x + 1987 / 2) + 1987 / 2 = x + 1987, conflict with f(f(x)) = x + 1987 so f(x) <= x + 1987 / 2 , this is conclusion 2 combine conclusion 1 and 2: f(x) = x + 1987 / 2 f(0) = 1987 /2 is not integer, conflict with f(x) belong to Z so such f(x) not exist

I used your second method - knowing that powers of x+1/x to the 2ⁿ "look nice"! Your final explanation should have mentioned that if the two "powers" are adjacent (e.g. 3 and 4 or 11 and 12) you get an x+1/x term in the middle. Which is perhaps easier than dealing with (e.g. 2 and 5) x³+1/x³ in the middle.

I did it differently. A combination of my version after your "power of ten" extraction would have been quickest. (Find the 1000100010001 then long divide). GCF: divide greater by smaller until remainder = 0 (so old remainder becomes new divisor) the last divisor is the GCF Clearly a factor of 1000 can be taken out of the denominator 𝟸𝟸𝟺𝟺𝟾𝟻𝟷𝟺𝟾𝟻𝟷𝟺𝟾𝟻𝟷𝟺𝟼𝟸𝟽 𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾 ×𝟸𝟶𝟶 𝟷𝟼𝟸𝟹𝟽𝟼𝟸𝟹𝟽𝟼𝟸𝟹𝟽𝟼𝟸𝟹𝟼𝟶𝟶 - 𝟼𝟸𝟷𝟶𝟾𝟿𝟷𝟶𝟾𝟿𝟷𝟶𝟾𝟿𝟷𝟶𝟸𝟽 𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾 ×𝟽𝟶 𝟻𝟼𝟾𝟹𝟷𝟼𝟾𝟹𝟷𝟼𝟾𝟹𝟷𝟼𝟾𝟸𝟼𝟶 - 𝟻𝟸𝟽𝟽𝟸𝟸𝟽𝟽𝟸𝟸𝟽𝟽𝟸𝟸𝟽𝟼𝟽 𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾 ×𝟼 𝟺𝟾𝟽𝟷𝟸𝟾𝟽𝟷𝟸𝟾𝟽𝟷𝟸𝟾𝟽𝟶𝟾 - 𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿 𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾 𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿 𝚡𝟸 𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾𝟾𝟷𝟷𝟾 - 0 𝚐𝚌𝚏 = 𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿 𝚜𝚘 𝚌𝚊𝚗𝚌𝚎𝚕 𝚝𝚘𝚙 𝚊𝚗𝚍 𝚋𝚘𝚝𝚝𝚘𝚖 denominator = 2𝚡1000 numerator : 𝟸𝟸𝟺𝟺𝟾𝟻𝟷𝟺𝟾𝟻𝟷𝟺𝟾𝟻𝟷𝟺𝟼𝟸𝟽 𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿 𝚡𝟻𝟶𝟶 𝟸𝟶𝟸𝟿𝟽𝟶𝟸𝟿𝟽𝟶𝟸𝟿𝟽𝟶𝟸𝟿𝟻𝟶𝟶 - 𝟸𝟷𝟻𝟷𝟺𝟾𝟻𝟷𝟺𝟾𝟻𝟷𝟺𝟾𝟻𝟷𝟸𝟽 𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿 𝚡𝟻𝟶 𝟸𝟶𝟸𝟿𝟽𝟶𝟸𝟿𝟽𝟶𝟸𝟿𝟽𝟶𝟸𝟿𝟻𝟶 - 𝟷𝟸𝟷𝟽𝟾𝟸𝟷𝟽𝟾𝟸𝟷𝟽𝟾𝟸𝟷𝟽𝟽 𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿𝟺𝟶𝟻𝟿 𝚡𝟹 𝟷𝟸𝟷𝟽𝟾𝟸𝟷𝟽𝟾𝟸𝟷𝟽𝟾𝟸𝟷𝟽𝟽 - 0 𝟻𝟻𝟹/𝟸𝟶𝟶𝟶

No wonder this was double starred and put last on the test. Unless you are aware of "Vieta jumping" the chances of finding the solution in a short time are small. There's even a Wikipedia entry which solve this.

Much the same but slightly differently ... natural numbers s.t. 1<a<b<c and P=(a-1)(b-1)(c-1) | abc-1 or k(a-1)(b-1)(c-1) = abc-1 ...(1) ...(1) => k<abc/( (a-1)(b-1)(c-1) ) ...(2) note that for any natural number n>1, we have n/(n-1)>(n+1)/n (because n²>n²-1) and a≥2,b≥3,c≥4 so max value of ...(2) is for min, a,b,c from ...(2) k<24/(6)=4 k≤3 k=1 => ac+bc+ab-a-b-c=0 but ab > a and bc > b and ac > c, so k≠1 looking at a, if a≥4 k=(a/(a-1))(b/(b-1))(c/(c-1))-1/P ≤ (4/3)(5/4)(6/5)-1/P < 2 so no solution for a≥4 if a=3 k≤(3/2)(4/3)(5/4)-1/P < 2.5 so k=2 first consider a=2 k≤(2/1)(3/2)(4/3)-1/P < 4 so k=2 or 3 if k=3, 3(2-1)(b-1)(c-1)=2bc-1 3bc-2bc-3b-3c+3+1=0 bc-3b-3c+4=0 add 5 and factorise (b-3)(c-3)=5 factor pairs 1,5 solutions a,b,c = 2,4,8 if k=2 2(2-1)(b-1)(c-1)=2bc-1 -2b-2c+3=0 2b+2c=3 has no solutions for b,c > a=2 consider a=3 and k=2 2(3-1)(b-1)(c-1)=3bc-1 4bc-4b-4c+4-3bc+1=0 add 11 and factorise (b-4)(c-4)=11 factor pairs 1,11 solutions a,b,c = 3,5,15

This is a beautiful problem: At the solution, Can you say that actually, a = 1. … and then it’s a little suspect what youre doing with this. Since one is summing over integers strictly not on the prime ideal, The denominator isn’t carrying factors of this prime. So youre looking at a rational: something in lowest form 1979/… … by just observing its definition: No spooky logic implied, Doesn’t have any factors of this prime. … which makes me think its not too good of a problem after all these years.. I know thats not what theyre asking. It’s interesting to see if you can find this symetry elsewhere in this summation to find out if one can write this as 1979*a where a isn’t actually 1: This would beget spooky logic. If 1979 isn’t actually a prime: then none of this holds … - but one can’t be unsure about this pre-argumentation The only thing one can call beautiful is: The sameness between (1) Taking away a subsequence, additively (2) giving that same sequence, additively, whilst taking away .. the ring element ‘2’ multiplied by the same thing one is giving. This is the kind of trick one is using here.

I love the content

this is brilliant

can anyone explain how he got the numerator to be 1979 in the summation?

Eh am I stewpid or shouldn't it be 1+½+...+1/1319 - ½(1+½+...+1/658) instead of -2(...). Also there are so many mistakes (as you've noticed) that make this simple step redundantly hard to understand.

ummm, a much easier approach, or the most "visible" one; simply (x+1/x)³-3(x+1/x)=x³+1/x³ or 216-3(6)=198..... thats it

The more difficult version is the set of such sequence of 1's is never a perfect prime power

If n-m must be multiple of 100 (i.e. n-m≥100) and also m≥1, doesn't that mean that min(n+m) is for n=101 and m=1, thus min(n+m)=102? And obviously 101=n≥3, so that also checks out in this case, so isn't the answer 102 instead of 106 or am I missing something?

Лемма Титу.

Keep in mind "an Asian" Is solving this!

Given the condition that y≥4 at 2:43 then the corresponding solution at 3:30 should indeed be (y,z)=(2t,3t), where for t∈ℕ, but only for t>1 (for t=1 => y=2<4). But one might then think "but (x,y,z)=(1,2,3) is obviously a solution". Yeah, but it's a result from the solution found at 6:46, not the one at 3:30

I think was a very easy imo problem.

The expansion of (a(x+1)+b)(cx+d) at 5:30 should have a bcx term instead of the bdx term shown in the video

do i have any problem for this solution? since proven f is 1-1 and f(x+1987)=f(x)+1987, then f(x+1987)-f(x)=1987, hence f is a linear function (since the difference between every set of (x,x+1987) must be a constant), which x>0. Then, since f(f(x))=x+1987, m(mx+b)+b=x+1987, which we can get m=1,-1(rejected) and b=1987/2. considering that previously we know x>0 and f defined in Z>0, then looking back to the f(x)=x+1987/2, which firstly f is not integer for integer inputs, and it is also not defined in [0,1987/2). Therefore, we can claim that no such function.

I've created 2 years ago a shortcut for such math problems: √[n (n+1) (n+2) (n+3) + 1] ------> for 4 consecutive numbers + 1 5n + (n -1 )^2 --------------------- 5 * 1000 + 1000000 - 2000 + 1 = 1000000 + 3001 = 1003001

LHS must be even assuming it's not an even prime (but p=2 works too) so then RHS is odd, meaning it's congruent to 0 mod 4. Therefore p^3 + 1 = 0 mod 4 so p must be 3 mod 4, and primes must be 1 or 5 mod 6, so then p must be 11 or 7 mod 12. The only primes generated by this are 7,11,19,23,31, and 43 and checking yields p = 7,11 (it's annoying if you don't have a calculator but very doable with some mod checks + divisibility checks, eg if it's congruent to 0 modulo by n and not n^2 where n is not a perfect square then it cannot be a perfect square)

I've the easiest and shortest method. It can be solved in a minute or two.

How about using weirstrass inquealitiy considering a2a3......an=1 but its not given that a2a3........an<1

bro is insane

czcams.com/video/7-GkLcIZqiQ/video.html outstanding!!!

Where is 1/659?

I didn't grab a finer point: how you went from 2^(x-1) congruent to 0 mod 8 to y+1+2^(x-1)=7*2^(2x-3). Can someone explain why k must be 2x-3, not 2x-1 or 2x+7 and so on?

Another approach without using modulo and log (this is "no-pen-no-paper" method): 1. the last digit of x must be 9, because only 9 goes in cycles (9,1) with the 13th power being 9. 2. 100^13 is 27-digit number, so x must be 2-digit number ----> 26(digits) : 13 = 2. 3. x can't be 99, because the given 26-digit number is too small (it's obvious). 4. 8 = (2^3)^13 = 2^39; let's calculate 2^40 5. 2^10 = 1024, let's use "1000" 6. 2^40 = approx. 8^13 = approx 1000 ^4 7. 80^13 = approx 1000 ^4 * 10^13 = 10^12 * 10^13 = 10^25 8. It is less than the given 26-digit number 9. therefore x = 89

How would you choose the squares if you got something like m^4 + 3m^3 + ... with the cubic term

I got lost on the sumation part (note im finishing calc 1 so xd)

Two cool facts about 13th powers is that a) the answer is approximately 13 times the length of the number; and b) that the last digit is always the last digit of the number we’re after… Given this, we can confidently say this is a two digit number ending with 9 (26 digits long, very convenient!), given 100^13 has 27 digits! The digit sum is not divisible by 3 or 9, so that leaves 39, 69 and 99 out… Another trick to know is that for 13th powers the second to last digit (which we can call x) can be used to determine the second to last digit of the root… in the case of a digit ending with 9, the value of the root’s second to last (technically first) digit would be 7(x-2) mod 10… equal to 7 x (6-2) mod 10 = 8… that would mean in our case that the 13th root of our number is 89…

Can someone help me with where 2p<=q+6 comes from? Thank you!

Vieta jumping and we done

And why did you add u? When you can easly 1²-2×1×√2+1+(√2+1)²

ทำไปแล้ว

Hk?

(3,4,5) and (3,5,6) and (4,3,5) and ( (4,5,3) and (5,3,4) and (5,4,3) is Solution. => n! Is Solution for n= 3, 3!=6 => For one Solution => 6 add. Total 30 solutions combined

Couldn't A1 = B ? Because if it could, then we don't have a contradiction.

My solution : If you subtract 1 from a multiple of seven , that number will either be odd or factor into an odd * even . As 2^n is always even * even we can never have this relation .

My solution : If you subtract 1 from a multiple of seven , that number will either be odd or factor into an odd * even . As 2^n is always even * even we can never have this relation .