
- 9
- 278 511
jHan
United States
Registrace 10. 01. 2021
Mathematics can sometimes be frustrating and unintuitive. This channel seeks to explain and express mathematical concepts and ideas in a beautiful, intuitive way. Animations are made with 3Blue1Brown's animation engine Manim: github.com/3b1b/manim
The Axiom of Choice
Mathematics is based on a foundation of axioms, or assumptions. One of the most important and widely-used set of axioms is called Zermelo-Fraenkel set theory with the Axiom of Choice, or ZFC. These axioms define what a set is, which are fundamental objects in mathematics. And the Axiom of Choice is arguably one of the most important and interesting axioms of ZFC. But what does it really say? And how is it used? This video dives deep into the formal definition of the Axiom of Choice, as well as its important equivalences which have their own fascinating applications in various branches of mathematics. Furthermore, we look into the controversy behind AC, and why it has garnered much discussion throughout its mathematical history.
0:00 Introduction
1:28 Set Theory and ZFC
9:22 The Axiom of Choice
16:55 Zorn's Lemma
23:39 The Well-ordering Theorem
27:49 Other Equivalences of AC
29:23 Controversy & Final Thoughts
Additional Resources:
The Banach-Tarski Paradox by Vsauce: czcams.com/video/s86-Z-CbaHA/video.html
Wikipedia article on the Axiom of Choice: en.wikipedia.org/wiki/Axiom_of_choice
Wikipedia article on ZFC: en.wikipedia.org/wiki/Zermelo%E2%80%93Fraenkel_set_theory
Music:
c418.bandcamp.com/album/dief
Smooth Fall by C418
Work Life Imbalance by C418
c418.bandcamp.com/album/life-changing-moments-seem-minor-in-pictures
In Berlin people act differently by C418
c418.bandcamp.com/album/seven-years-of-server-data
The first unfinished song for the Minecraft documentary by C418
patriciataxxon.bandcamp.com/album/aeroplane
Cribwhistling by Patricia Taxxon
Starboard by Patricia Taxxon
Animations were made by Manim, an open-source python-based animation program by 3Blue1Brown.
github.com/3b1b/manim
0:00 Introduction
1:28 Set Theory and ZFC
9:22 The Axiom of Choice
16:55 Zorn's Lemma
23:39 The Well-ordering Theorem
27:49 Other Equivalences of AC
29:23 Controversy & Final Thoughts
Additional Resources:
The Banach-Tarski Paradox by Vsauce: czcams.com/video/s86-Z-CbaHA/video.html
Wikipedia article on the Axiom of Choice: en.wikipedia.org/wiki/Axiom_of_choice
Wikipedia article on ZFC: en.wikipedia.org/wiki/Zermelo%E2%80%93Fraenkel_set_theory
Music:
c418.bandcamp.com/album/dief
Smooth Fall by C418
Work Life Imbalance by C418
c418.bandcamp.com/album/life-changing-moments-seem-minor-in-pictures
In Berlin people act differently by C418
c418.bandcamp.com/album/seven-years-of-server-data
The first unfinished song for the Minecraft documentary by C418
patriciataxxon.bandcamp.com/album/aeroplane
Cribwhistling by Patricia Taxxon
Starboard by Patricia Taxxon
Animations were made by Manim, an open-source python-based animation program by 3Blue1Brown.
github.com/3b1b/manim
zhlédnutí: 73 439
Video
Genius Mathematicians Lost Too Soon
zhlédnutí 2,7KPřed 10 měsíci
Some mathematicians changed the field of mathematics at a young age, only to die too early. Let us look at the lives of some of these young, brilliant minds who left too soon. Evariste Galois was a French mathematician who laid the foundations of abstract algebra and Galois theory, proving the quintic's insolubility. Srinivasa Ramanujan was an Indian mathematician who, upon his genius being dis...
But what is a Vector Space?
zhlédnutí 3KPřed 11 měsíci
Vectors are fundamental tools in mathematics and sciences. Yet different fields like mathematics, physics, and engineering seem to define vectors differently. It is mathematics, unsurprisingly, that formally defines a vector. We will go through this process of formalization, using the foundational tools of abstract algebra to define and construct a vector space. Additional Resources: Wikipedia ...
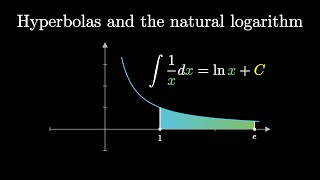
Why Logarithms Appear in This Integral
zhlédnutí 2,1KPřed rokem
Before the days of Calculus, one Pierre de Fermat wanted to find the area under the function f(x)=x^n. This problem we now call "integration" was then called "quadrature" or "squaring". Fermat was able to square every function f(x)=x^n for any rational n except for one case: n=-1 (that is, the hyperbola). It turns out that this unique nature of the hyperbola was tied to logarithms and Euler's n...
How to Find the Biggest Primes
zhlédnutí 8KPřed rokem
How do people find big primes? These primes have millions of digits, and may take years of collective effort and computing power to be found. Unsurprisingly, mathematicians have figured out various ways to more efficiently and accurately find these big primes. In the process, the unique and interesting properties of various primes have also been found. Great Internet Mersenne Prime Search: www....
Cardinality of the Continuum
zhlédnutí 52KPřed rokem
What is infinity? Can there be different sizes of infinity? Surprisingly, the answer is yes. In fact, there are many different ways to make bigger infinite sets. In this video, a few different sets of infinities will be explored, including their surprising differences and even more surprising similarities. 0:00 - Euclid's Proof of Infinite Primes 1:55 - Bigger Infinities? 2:27 - Set Theory and ...
The Cardinality of an Interval
zhlédnutí 2,7KPřed 2 lety
Cantor's Diagonal Argument proves that there are an uncountable number of real numbers. But what about any interval of real numbers? Are those sets uncountable as well, no matter how small the interval?
Can the power of two irrationals be rational?
zhlédnutí 4,1KPřed 2 lety
Are there two irrational numbers, let’s say x and y, such that x to the y is rational? The answer to this question brings us through a fascinating journey about transcendental numbers and the Gelfond-Schneider theorem. Additional Resources: Where I found this theorem: math.stackexchange.com/questions/728223/simple-beautiful-math-proof/728276 Music: www.purple-planet.com Animations were made by ...
Why do trig functions appear in Euler's formula?
zhlédnutí 131KPřed 2 lety
Why do trig functions appear in Euler’s formula? This was the question I had when I first saw Euler’s formula. This connection between trigonometry and exponents seems so unexpected, especially along with complex numbers. To answer this question, we must journey into the intricate and beautiful mathematical relationship between trig functions, e, and complex numbers. We will look at two differe...








the title of this video sounds like star trek fanfic
What's the music at @8:25? Great video by the way
2:05 oh ... jHan is freaking cute.
32:04 _Even if we know there is a limitation_ _That doesn't mean we can't reach New Heights_ -jHan
are there books or resources you recommend that dive deep into set theory?
amazing detailed video !
This video was concise and to the point. Clear information bundled up tight.
Excellent video, but highly distracting music
i knew about the way Andrew Wiles proved Fermat's Last Theorem but i never knew what happened to Taniyama. Him and Shimura saw a turbulent time not just for the world but for their country. Rest in peace.
Superb video, a work of art. Super easy to follow - you guide us well through these topics. Thank you.
You forgot to mention the Axiom of Determinacy.
what book/lectures do you suggest to go into more details about ZFC set theory ?
Gödel
Arithmetic cannot be completed (Incompleteness), but it can only be described robustly within multiplication. Unlike Addition, Multiplication requires its Elements to be identical for validity. Under Multiplication the Integers are a finite, but unending population of slopes, no longer fully infinite.
Woah woah woah. No. Banach Tarski is implied by *_Hahn Banach._* It's strictly weaker than Choice. And you can't do Functional Analysis without Hahn Banach. It's a fool's errand. Banach Tarski is a demon that cannot be exorcised.
Abstract algebra not only contain meaningful abstractions and meaningless ones, so in conclusion not only they are undecidable but also fail to arrive at meaningful objects. As for other branches of mathematics the theorems of abstract algebra doesn't apply.
who is the audience for this? i can’t really see how this would teach anybody who wasn’t already familiar with these topics anything. Within minutes of explaining what a set is you’re already busting out set theory jargon with very few examples a layman would understand.
Really needed this about 4 months ago
Brilliant 🎉 video. I would like to make a suggestion, that being a video on tensor just like this having axiomatic definition. The reason I request is most of us students are clueless about what tensors is in mathematical stand point.
this was cool and inspiring
I appreciate that you gave a basic understanding of the terminologies, which where to be used in a statement. And as a person who forgets everything, I really appreciate your recap. Thanks.
2 sets are equal if they have same elements; so nature is sexist? ohh noo~~~
One thing that is quite important but often skimmed over is that axioms are not meant to be "obviously true". They are true within the framework of a theory, they are the "ifs" to the "thens" the theory shows. A theory does not assert them, it *requires* them. We needed to abandon this particular mindset that there is a single universal "mathematical truth" to discover so many new worlds, from complex numbers or infinite cardinalities to non-Euclidean geometry. If you find a situation where the axioms are actually true (like the real world), then you can happily apply the theory, but if not, it is equally valid to use it in a "what if" way.
Does it work for the set of all complex numbers?
What exactly do you want to know if it works? The set of complex numbers is just R ×R with appropriately defined + and * operators (the pair [a,b] is by convention written as a+b*i, and the complex numbers are added and multiplied as polynomials with i*i=-1). It can be shown that R ×R can be mapped one-to-one with R; the same is true for R^n for any natural number n - set of all n-tuples of real numbers for some finite n, as well as R^N - set of all infinite sequences of real numbers. Likewise, N^N and 2^N (set of all infinite sequences of natural numbers, or of digits 0 and 1) can be mapped one-to-one with R.
@@MikeRosoftJH i have low pressure and cant understand
@@mihaleben6051 And I don't know what exactly you're asking. What do you want to know if it works with complex numbers?
@@MikeRosoftJH nevermind. I dont need to know anymore.
What about |R^R| ? :-)
well, |R^R|>=2^|R|=|P(R)|>|R|
Superlative. Best teachers are on CZcams!
Great video, thank you for your work!! New sub here. Greetings from Argentina
14:32 The domain of h in this case doesn't have to be P(X)\{∅} right? It can just be the union of all Xy such that y belongs in Y.
Wow! Thank you so much for this extremely helpful video!!
Proving continuum hypothesis , proving inconsistency in ZFC , constructing ZFC from naive set specification , resolving Russell's paradox , constructing infinite number system , construct and ensure overall consistent mathematical universe and developing arithmetic system - edition 8 May 2024 DOI: 10.13140/RG.2.2.21713.75361 LicenseCC BY-NC-ND 4.0
Good video, but several typos throughout, especially regarding names (for example 2:30 has Russel instead of Russell, 4:20 has Bernsays and Godel instead of Bernays and Gödel). You also pronounced "Neumann" as "Newman", rather than the correct "Noyman" at 3:02.
HELLA BEAUTIFUL!
Does the definition of bijective functions guarantee that all bijective functions are monotonic?
Absolutely not; in fact, it's not given that a "canonical" ordering on that set exists at all. For example, the set of all functions on real numbers (R^R) can be mapped one-to-one with the set of all sets of real numbers (2^R). Now can you give me an ordering on either of these sets? You can't - that any ordering relation on the set exists is a consequence of of the axiom of choice (just like that R can be well-ordered is a consequence of the axiom of choice). I'll give you a trivial counter-example: consider the set {1,2,3,4}, and the function: [1,2,3,4] -> [1,2,4,3]. It can be seen that this function is neither strictly increasing nor strictly decreasing. Likewise (for a somewhat less trivial function): consider the function on an interval of reals from 0 to 1: f(x) is obtained from x by swapping the first two digits after the decimal point. (So for example 0.121212...=12/99 will be mapped to 0.21121212... . For lack of ambiguity, in case of a number like 1/10 we will use the decimal expansion 0.1000... and not the alternate expansion 0.0999...; so f(0.1)=0.01 and not 0.90999...=0.91.) Again, it can be seen that this is a one-to-one function, but it's not monotonous on its domain.
This is magic
One of the best out there!
Two key points in the video were when you mentioned ordinals and chain
Banach-Tarski has bothered me a lot less since I realized that, given that planar construction geometry as per Euclid, only points with rational coordinates are in the constructible plane. So there are uncountably infinitely many holes in a continuous plane already. What's a few more? I suppose it would take a lot of work to try to figure out just how many intuitive and even axiomatic assertions there are because the Euclidean plane is quite literally nothing compared to a continuous plane.
Minor nitpick: square roots of constructible numbers are constructible, so there are some points with irrational coordinates which are constructible, e.g., (sqrt(2),sqrt(2)). Nevertheless, your main point stands: it is still true that there are only countably many constructible points on the plane. This follows from the fact that all constructible numbers are algebraic and there are only countably many algebraic numbers.
@@MuffinsAPlenty Yes; you're quite right. Still, there are either ℵ₁ or ℵ₂ holes, depending on what you prefer. I like CH because it lets me sort of visualize up to ℵ₄ on a good day. I leave the idea of whether this has anything to say about classical versus quantum physics to the reader.
@32:00 lovely closing outro. But if these are "truths" they are not necessarily truths about "our universe" --- if by that you mean physical spacetime. The V of mathematics is different to the U of physics. Probably. ;-) If so, mathematics has this power to take a mind beyond physics. At least I've always thought so. (Banach-Tarski is not about physical bolls).
One of the deeper problems here is "logicism". Mathematics is richer than that and is a system _with which we we formalize_ basic numerical and geometric _intuitions._ But the intuitions are often thought to be "not mathematics". This is wrong, and yet true in one sense: our intuitions are not _formal mathematics._ One intuition is that if we throw a (mathematical point) dart at the line ℝ it will hit a real number (or a hyperreal that has a real _standard part_ ). Mixing such physics/geometric notions with formal mathematics is considered by math snobs and level-2 nerds to be a terrible "no no" but that's the problem. Logicism or formality restricts axiomatic development and gives rise to some of the unintuitive results. But the restrictions are a good thing, they give more creative mathematicians room. Creating better formal mathematics out of basic intuitions is the task. No one said it could be perfected.
Sets feel like "who's on first." The math that I don't like is where physicists think math can dictate cause to them. To get a physics degree, everything is 100% math. Cause is an afterthought scoffed as "the intuitive explanation," and yet I can prove that dancing around math analogies can hide the real cause from you. "The wheels on the bus go round and round." This song describes EVERYTHING you see a bus do exactly like math does, but it is not an understanding of a bus. Modern science WILL NOT see past the FIRST successful description. Constants are SET in stone. You think angular momentum causes the gyroscopic effect, and it is well known that angular momentum is a fake vector. Make sense of that one. I have a video that shows what cause actually looks like, and it's based in absolutes.
For some reason this is the first time Ive come across the double-representation edge case, really interesting 👍
Wait, you never participated in "is zero nine repeating equal to one" debates on youtube???!!! 😱
@@allozovsky nonono of course I have, I mean in the context of cantor's diagonalization. Its a very serious loophole
@@alegian7934 Some college/university level math books simply treat this representation as _not valid:_ *Definition.* Let's call an infinite decimal expansion _valid_ if it does terminate with 999... *Lemma.* There is a one-to-one correspondence between the set of all real numbers and the set of all _valid_ infinite decimal expansions: I do not know how common this approach is, though. I'm still getting used to this new to me "definition", which seems to somehow "deassign" the value of *0.999...,* making a question "what it equals to" sort of pointless.
Axioms are not “true”. This is a meaningless phrase. Axioms are just a assumed so that the logical consequences of that assumption can be explored
Great video man, you are gonna blow up for sure!
Something is wrong. How come I wasn't subscribed to this channel yet!!?? This video is great!!!
bro thinks hes 3Blue1Brown😹😹😹
Was about to say how great this video was, but then saw you include 0 in the natural numbers.
One of the easiest bijections between (0, 1) and R is y=tan(pi*x)
*y(x) = tan⁻¹(x)/π + 1/2* looks nicer (though essentially the same, of course)
Great info but the muzak is distraction.
Mathematics
5:37 okay I'm completely lost
Can we build maths on the category theory instead of set theory?
Yes we can, you can read “joy of cats”
This is duality; Injective is dual to surjective synthesizes bijection or isomorphism. Absolute truth is dual to relative truth -- Hume's fork. Syntax is dual to semantics -- languages or communication. Categories (form, syntax, objects) are dual to sets (substance, semantics, subjects) -- category theory. If mathematics is a language then it is dual. All numbers fall within the complex plane. Real is dual to imaginary -- complex numbers are dual. All numbers are dual! The integers are self dual as they are their own conjugates. "Always two there are" -- Yoda. Subgroups are dual to subfields -- the Galois correspondence.
@@hyperduality2838🤓